statistika

Co je to statistika?

Význam slova statistika

V první řadě je třeba podotknout, že slovo statistika má významů hned několik. Je pravděpodobné, že jako první z nich přijde čtenáři na mysl statistika jako vědní disciplína, což je právě význam, o kterém pojednává tato kapitola. Druhý význam je statistika jako vypočtený kvantitativní ukazatel nějaké vlastnosti náhodné veličiny ve zkoumaném statistickém vzorku. Pod touto obšírnou definicí se skrývají i veskrze prosté údaje, jako například aritmetický průměr či medián. Třetí význam, spíše hovorový, představuje statistika jako označení statistické analýzy. Bohužel pro nás statistiky tedy nestačí na prosbu kolegy: „Udělej mi prosím statistiku těch nových dat,“ vypálit od boku aritmetický průměr a považovat tím žádost spolupracovníka za vyřešenou.

Co statistika řeší?

Nyní ale již zpět ke statistice jako vědní disciplíně. Krom pozice vyhlášeného strašáka v učebních osnovách má statistika nezastupitelnou roli všude tam, kde se člověk setkává s daty, především pak s potřebou zjistit, co mu tato data říkají a říci mohou. A to je o statistice ta nejdůležitější a zároveň (nejspíše pod tíhou vzorců a výpočtů) i ta nejopomíjenější skutečnost – úkolem statistiky je vytěžit z dat informace v nich obsažené a podat je uživateli ve snadno uchopitelné, ať už numerické (číselné hodnoty) nebo sémantické (odpověď na otázku, tvrzení) formě. Budeme-li na tento přístup pamatovat, usnadníme si tím zásadním způsobem orientaci ve statistice, neboť už si nadále nebudeme pokládat otázku: „Co všechno musím vypočítat?“, a následně zásobovat čtenáře či posluchače tučným přísunem čísel, ale naproti tomu se vydáme na detektivní dráhu s otázkou: „Jak zjistím odpověď?“ a pokusíme se dobrat k závěrům jednoznačným, jednoduchým a přehledným.

Tento přístup často znamená méně výpočtů, méně formalit a v některých případech i méně samotné statistiky, především při prezentaci dat. Někdy za sebe data totiž mluví nejlépe sama, a to skrz naši zkušenost s jejich vnímáním. Nikdo z nás totiž nepotřebuje statistický test na vyhodnocení pětikilogramového nárůstu tělesné hmotnosti zjištěného v prvním lednovém týdnu. A v tomto duchu bude pojatý i následující text.

Pravděpodobnost a statistika

Tyto dva blízce provázané obory – pravděpodobnost a statistika – se často vyskytují společně, často dokonce jako název studijního předmětu, když se s nimi setkáváme poprvé. Podobně jako psaní a čtení, které se zprvu učíme společně, se při dalším studiu naučíme tyto disciplíny rozlišovat, vnímat a studovat odděleně, což ovšem nic neubírá na intenzitě jejich spojení. I vzájemný vztah těchto oborů je analogický. Pravděpodobnost studuje způsob, jak za nevyhnutelného přispění náhody data vznikají. Tato data představují text, do kterého jsou prostřednictvím experimentu či měření zapsány informace o realitě. Statistika se pak učí data číst a obsažené sdělení a zákonitosti do nich promítnuté pochopit. Navíc, stejně jako čtení a porozumění textu probíhá na různých úrovních, tak i statistika vyžaduje ryze formální a technické nástroje (vypočítat hodnotu dané statistiky nebo určit typ dat – podobně jako rozeznat jednotlivá písmenka, slabiky, slova) doplněné vyšší úrovní pochopení významu a abstrakce.

Data a jejich typy

Co jsou to data?

Naměřená data představují konkrétní zjištěné hodnoty jedné nebo více náhodných veličin. Náhodná veličina je číselným vyjádřením výsledku náhodného jevu, který souvisí se zkoumanou vlastností subjektu či statistického souboru. Náhodnost takové veličiny znamená, že při opakovaném měření nabývá vlivem neznámých nebo neovlivnitelných náhodných činitelů1 různých hodnot, přestože zajistíme neměnné podmínky měření. Prostřednictvím statistické analýzy se pak často snažíme část náhodné variability této veličiny vysvětlit, ale nepředbíhejme.

Protože nedílnou součástí získávání dat je krom samotného studovaného jevu také proces měření, setkáváme se v praxi se dvěma zdroji náhodnosti v datech, a to s vlastní variabilitou zkoumané veličiny a s náhodnou chybou měření. V závislosti na konkrétní úloze pak mohou nastat dva scénáře. V prvním případě, podrobně studovaném v metrologii, předpokládáme, že existuje jediná pravdivá hodnota měřené veličiny (ta tedy není náhodná), ale výsledek měření, představující součet měřené veličiny a náhodné chyby, již náhodnou veličinou je. V druhém případě, s nímž se při zpracování dat potkáme častěji, je náhoda přímou součástí měřeného jevu a spolu s náhodnou chybou měření ovlivňují variabilitu získaných dat společně. Při návrhu experimentu je pak vždy nutné pečlivě zohlednit vzájemný poměr obou těchto vlivů. Nejpříjemnější situace pochopitelně nastává, je-li chyba měření vzhledem k přirozené variabilitě měřené veličiny (a také intenzitě případného vlivu, který zkoumáme) zanedbatelná.

Kategorie dat

Před zpracováním dat je nezbytné si uvědomit, jakou povahu naše data vlastně mají, což nám značně zjednoduší zacházení s nimi. Daná veličina tedy může být:

•Kvalitativní (kategorická)

onominální – vyjadřuje příslušnost prvku či jedince k nějaké kategorii (například pohlaví, povolání, zdravý/nemocný, experimentální skupina/kontrolní skupina, léčba zabrala – ano/ne)

oordinální – představuje kategorie, které je možno seřadit podle závažnosti, intenzity apod. (například známky ve škole, grade tumoru, energetická třída ledničky).

Pozor, případné číselné vyjádření názvu kategorie nepředstavuje hodnotu veličiny. Ve škole tak máte trojku, protože se tak jmenuje, nikoli proto, že by to byly tři jednotky „něčeho“.

•Kvantitativní (číselné)

odiskrétní – vyjadřuje počet celých, nedělitelných jednotek dané veličiny (např. počet dětí, počet záchvatů mezi kontrolami)

ospojitá – nabývá libovolné přípustné hodnoty (např. hmotnost, krevní tlak, věk, teplota).

I když v praxi nám měřicí přístroj s nevyhnutelně omezenou rozlišovací schopností poskytuje konečný počet zaokrouhlených, kvantovaných hodnot, nebudeme se touto skutečností trápit a veličinu budeme dále považovat za spojitou.

Zvláštní pozornost je třeba věnovat jedné veličině (můžeme ji však považovat i za statistiku), a tou je četnost. Četnost (ať již relativní nebo absolutní) udává, kolik hodnot daného znaku se vyskytuje ve vzorku či populaci. Z hlediska výše uvedené klasifikace je absolutní četnost diskrétní kvantitativní veličinou, ale může vznikat z dat libovolné povahy, čímž nám v některých případech umožňuje ostatní druhy veličin do této kategorie převést. To může být jak výhodné (například při prezentaci dat), tak nevhodné (při použití některých testů).

Příklad: V rámci experimentu byla testována klíčivost semen. Celkem bylo nasazeno osm misek po deseti semenech. Na čtyřech miskách vyklíčilo 9 z 10 semen a na zbývajících čtyřech 8 z 10. Na výsledky experimentu můžeme pohlížet všemi následujícími způsoby:

1.semeno 1: vyklíčilo, semeno 2: vyklíčilo, semeno 3: nevyklíčilo, … (Evidujeme tedy 80 jedinců a hodnotu nominální veličiny „vyklíčilo/nevyklíčilo“.)

2.celkem vyklíčilo 68 z 80 semen, zjištěná klíčivost je proto 85 %. (Experiment popisujeme celkovou četností.)

3.bylo změřeno celkem 8 hodnot klíčivosti – 80 % (miska 1), 80 % (miska 2), 80 %, 80 %, 90 %, 90 %, 90 %, 90 %. Průměrná klíčivost tedy je 85 % se směrodatnou odchylkou 5,35 %. (Používáme četnosti systematicky seskupených měření.)

Nelze kategoricky tvrdit, který způsob je správný, záleží vždy na okolnostech. Třetí případ může být uplatněn v situaci, kdy se semínka na misce vzájemně ovlivňují (například při napadení plísní je postižena celá miska) a seskupení po miskách je opodstatněné. Pokud však plánujeme provádět statistické testování hypotéz, je nutné brát v potaz, že pro kategorické a číselné veličiny používáme jiné testy a také že seskupení dat pomocí četností radikálně snižuje počet měření a tím i sílu testu. Zatímco v prvním případě máme 80 měření s výstupem ano/ne, ve třetím případě pouhých 8 měření kvantitativní veličiny. Druhý případ představuje jediné měření a nemůžeme jej tedy pro testování hypotéz (ani například pro výpočet směrodatné odchylky) použít.

Zaznamenávání a ukládání dat

V dnešní době je standardem elektronické uchování dat ve formátu tabulky, ať již v nejrozšířenějším tabulkovém editoru MS Excel, nebo v alternativních editorech (Open Office / Libre Office – Calc, Tabulky Google) či specializovaných softwarových produktech. I v této oblasti se však můžeme dopustit některých chybiček, které nám následnou analýzu dat komplikují.

Nejjednodušší bude využít následujícího příkladu:

Na dvou laboratorních myších byla otestována léčebná procedura. Vitalita myší byla ohodnocena stejným způsobem před a po léčbě. Výsledná data můžeme zaznamenat různými způsoby; dva příklady jsou uvedeny v Tab.1 a Tab. 2.

Tabulka 1: Příklad záznamu dat experimentu

číslo měření	zvíře	před/po	index
1	myš A	před	5,5
2	myš B	před	5,7
3	myš A	po	7,3
4	myš B	po	6,9

Tabulka 2: Příklad záznamu dat experimentu

zvíře	index před	index po
myš A	5,5	7,3
myš B	5,7	6,9

Obě tabulky obsahují totožná data, nicméně z hlediska následného zpracování je mnohem vhodnější ta druhá. Zde je několik důvodů:

oje výrazně méně rozsáhlá

onevyžaduje dodatečnou proměnnou (číslo měření) k jednoznačnému označení řádků

okaždá myš má právě jeden svůj řádek, kde jsou veškerá její data

Tabulky tedy nejčastěji sestavujeme tak, aby jednotlivé případy, tj. konkrétní pacienti, respondenti, zvířata a podobně, byly na samostatných a jedinečných řádcích. Proto se termín případ často používá pro označení řádku tabulky se statistickými daty.

Do sloupců pak zapisujeme hodnoty změřených veličin, tedy proměnných (rovněž zavedený termín, tentokrát logicky pro sloupce tabulky). Z našeho myšího příkladu je už čtenáři jasné, že není zdaleka neobvyklé, když se jedna, technicky vzato stejná veličina (například index vitality u myši, hmotnost pacienta apod.) v tabulce vyskytne rozdělena ve více proměnných, když si to logika a podmínky experimentu žádají (například index před léčbou a po, předporodní / poporodní hmotnost atd.).

Během sběru dat se nám často přihodí, že některý údaj není pro daný subjekt k dispozici (výpadek měřicího přístroje, předčasný úhyn pokusného zvířete apod.). V tomto případě není nutné vyřazovat celý subjekt z našeho vzorku, protože může být stále užitečný v analýzách, kde danou hodnotu nebudeme potřebovat. Existují také postupy, kterými je za určitých okolností možné chybějící hodnotu nahradit v případě, kdy se bez dané proměnné neobejdeme. Každopádně je ale nezbytné s jistotou vědět, že v daném políčku tabulky je právě chybějící hodnota. Z tohoto důvodu je třeba takové políčko označit jednoznačným a předem dohodnutým kódem (např. „XXX“, „?“, „chybí“, „---“). Není vhodné nechávat políčko prázdné (nebudeme vědět, jestli jsme jen hodnotu nezapomněli vyplnit). Pokud se jedná o číselnou proměnnou, není za žádných okolností přípustné použít jako kód chybějící hodnoty nulu, velmi pravděpodobně by došlo k záměně za nulovou hodnotu dané proměnné namísto zamýšleného „hodnota neznámá“.

Hodnoty kategorických proměnných je vhodné označovat stručně nebo zkráceně, abychom snížili riziko, že se v tabulce (například kvůli překlepům) objeví více různých označení pro tutéž kategorii.

Problematické jevy v datech

Ve většině datových souborů se pravděpodobně setkáme s chybějícími hodnotami. Nejjednodušším způsobem, jak se s chybějící hodnotou vypořádat, je vynechání příslušného subjektu (případu) z dané analýzy (tj. např. z jednoho konkrétního testu). Při výpočtu korelačních matic můžeme provést vynechání chybějících dat dvěma způsoby. Při vynechání celých případů (en. casewise deletion of missing data) jsou do výpočtu celé matice zahrnuty jen případy bez chybějících hodnot ve všech vyhodnocovaných veličinách. Párové vynechání dat (en. pairwise deletion of missing data) pak použije pro výpočet každého korelačního koeficientu v matici všechny případy s dostupnou hodnotou dané proměnné.

Existují také postupy, kterými je za určitých okolností možné chybějící hodnotu nahradit v případě, kdy se bez její hodnoty neobejdeme. Nejjednodušším způsobem je její nahrazení průměrem ostatních případů. Sofistikovanější metoda, založená na shlukové analýze, nejprve vyhledá několik případů s podobnou hodnotou ostatních proměnných a chybějící hodnotu nahradí průměrnou hodnotou příslušné veličiny vypočtenou z těchto případů.

Odlehlá pozorování (en. outliers) jsou naměřené hodnoty výrazně se lišící od většiny vzorku. Odlehlé hodnoty se mohou v datech vyskytnout jak následkem chyby při jejich měření či zaznamenání (špatný odečet hodnoty, překlep), tak náhodným výběrem netypického subjektu do našeho vzorku. Rozhodnutí, je-li určitá hodnota odlehlá, je do jisté míry individuální, a ať už jsou takové hodnoty určovány na základě matematického pravidla nebo manuálně, závisí jejich výběr především na kvalifikovaném odhadu experimentátora.

Stejně tak řešení výskytu odlehlých pozorování se neobejde bez kvalifikovaného lidského zásahu. Hodnoty velmi vzdálené od běžného rozsahu hodnot veličiny nebo hodnoty zcela nesmyslné je zpravidla užitečné ověřit ve zdrojových souborech z měření a pokusit se dosledovat vznik chyby během zpracování dat. Pokud se nepodaří chybu nalézt a opravit, můžeme hodnotu prohlásit za chybnou a nahradit ji chybějící hodnotou. Tento postup je však přípustný jen u zcela nesmyslných hodnot a nesmí být použit k eliminaci dat jen proto, že zjištěná hodnota nevyhovuje naší hypotéze. Je-li hodnota odlehlého pozorování v přípustných mezích pro danou veličinu, nezbývá zpravidla nic jiného, než se smířit s výskytem netypického subjektu v našem vzorku, toto pozorování v souboru ponechat a pamatovat na něj při volbě statistických metod pro další zpracování dat.

Statistická rozdělení

Rozdělení pravděpodobnosti, statistiky a parametry

Z povahy náhodné veličiny vyplývá, že její hodnoty se u jednotlivých subjektů v populaci liší. Rozložení hodnot náhodné veličiny v populaci (tedy zjednodušeně kolik subjektů vykazuje jakou hodnotu) nazýváme rozdělení pravděpodobnosti náhodné veličiny. Pravděpodobnosti proto, že vybíráme-li dokonale náhodně subjekty z populace do našeho statistického vzorku, udává rozdělení náhodné veličiny pravděpodobnost (či hustotu pravděpodobnosti u spojitých rozdělení), se kterou bude hodnota veličiny vybraného subjektu nabývat určité hodnoty. Z této vlastnosti vypovídá i skutečnost, že čím více subjektů náš vzorek obsahuje, tím spíše se rozdělení veličiny ve vzorku bude blížit jejímu rozdělení v populaci, což jsme již zmínili kapitole 1.3.

Abychom byli schopni stručně kvantitativně vyjádřit vlastnosti konkrétního rozdělení pravděpodobnosti, využíváme číselných ukazatelů - parametrů a statistik. Zatímco parametry popisují rozdělení veličiny v populaci, statistiky jsou odhadem těchto parametrů vypočteným z dat změřených na statistickém vzorku. Statistiky a parametry můžeme rozdělit podle toho, jakou vlastnost rozdělení vystihují. Polohové (en. location, central tendency) statistiky a parametry (např. aritmetický průměr, medián, modus, winsorizovaný průměr) udávají, jak vysoké jsou hodnoty, jichž veličina nabývá. Statistiky a parametry disperzní (směrodatná odchylka, rozptyl, mezikvartilové rozpětí) naopak popisují, jaká je variabilita veličiny mezi jednotlivými subjekty. Tyto dvě kategorie však nejsou vyčerpávající, další statistiky popisují například tvar rozdělení (šikmost, špičatost), nebo jsou využívány při výpočtu statistických testů. Některé statistiky jsou použitelné bez ohledu na rozdělení veličiny, jiné pak mají smysl jen pro určitá specifická rozdělení.

Statistika rozlišuje celou řadu různých rozdělení. Mohou být diskrétní pro diskrétní veličiny a kategorické veličiny (například pro hod kostkou, kde jsou přípustné hodnoty 1, 2, 3, 4, 5 a 6, ale nic mezi nimi) nebo spojitá pro veličiny spojité.

Centrální limitní věta a normální rozdělení

Nejdůležitějším spojitým rozdělením ve statistice je bezesporu rozdělení normální, hovorově nazývané také gaussovské, neboť hustota pravděpodobnosti normálního rozdělení je určená Gaussovou funkcí (křivkou). V angličtině se můžeme setkat i s nepříliš jednoznačným označením „bell curve“.

Normální rozdělení se v našem světě vyskytuje poměrně často (i když ne tak často, jak by si statistici přáli) díky platnosti takzvané centrální limitní věty, která popisuje následující jev. Již jsme si řekli, že vybíráme-li náhodný subjekt z populace, odpovídá rozdělení pravděpodobnosti hodnoty veličiny tohoto subjektu rozdělení náhodné veličiny. Představme si ale, že subjekty vybereme pokaždé dva, zjištěné hodnoty veličiny zprůměrujeme a výsledek zapíšeme jako jednu hodnotu. Rozdělení těchto průměrných hodnot se již bude od rozdělení původní náhodné veličiny lišit. Centrální limitní věta pak uvádí, že budeme-li počet zprůměrovaných vzorků zvyšovat k nekonečnu, bude rozdělení průměrných hodnot konvergovat k normálnímu rozdělení, a to pro jakékoli rozdělení původní náhodné veličiny (!). Původní rozdělení může být dokonce i diskrétní, neboť při průměrování nekonečného počtu vybraných subjektů se dostatečně „vyhladí“ a přejde do spojitého rozdělení normálního.

Jako příklad můžeme použít hod kostkou. Pro jeden hod je pravděpodobnost 1/6 pro každý výsledek z množiny {1, 2, 3, 4, 5, 6}. Budeme-li házet dvěma kostkami a výsledek průměrovat, rozšíří se množina možných výsledků na {1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5, 5.5, 6}, dojde tedy k částečnému vyhlazení původního diskrétního rozdělení. Zároveň začne pravděpodobnost růst pro hodnoty ve středu možných výsledků (pravděpodobnost výsledku 3.5 bude 1/6) a klesat pro hodnoty okrajové (extrémní výsledky 1 a 6 mají pravděpodobnost pouze 1/36). Pokračováním tohoto procesu průměrováním stále většího počtu hodů bychom se poměrně rychle přibližovali k normálnímu rozdělení.

Důvodem, proč nám tato zdánlivě nepodstatná věta přináší normální rozdělení tak často, je, že většina zkoumaných veličin je podmíněná celou řadou faktorů. Například IQ jedince je podmíněno značným množstvím faktorů genetických, výchovou, výživou, vzděláním a tak dále. Výsledná hodnota je tak v jistém smyslu průměrem těchto vlivů a její rozdělení proto tíhne k rozdělení normálnímu. Bohužel však tento princip nezřídka nefunguje zcela a nějaký silný demografický faktor či jiné okolnosti výsledné rozdělení od normálního více či méně odchýlí. Tato zpráva je špatná především proto, že většina běžných statistických metod byla vyvinuta právě pro normální rozdělení.

Vlastnosti normálního rozdělení

Jednou z důležitých vlastností normálního rozdělení je symetrie kolem střední hodnoty. Díky tomu je střední hodnota normálního rozdělení rovna aritmetickému průměru, mediánu i modu (nejčetnější hodnota) hodnot náhodné veličiny.

Další vlastností normálního rozdělení je neomezený definiční obor, jinými slovy je hustota pravděpodobnosti nenulová pro libovolnou konečnou hodnotu náhodné veličiny (nehraje roli, zda jde o hodnotu kladnou či zápornou). V tomto případě nastává často rozpor mezi teoreticky dokonalým normálním rozdělením a skutečným rozdělením náhodné veličiny (např. IQ, tělesná hmotnost), u které je v některých případech dosažení záporné hodnoty zcela nemožné. Ve většině těchto případů je však teoretická pravděpodobnost záporných hodnot naprosto zanedbatelná a normální rozdělení tak stále představuje dostatečně kvalitní model skutečného rozdělení takto omezené náhodné veličiny.

Statistiky a parametry normálního rozdělení

Normální rozdělení je plně definováno dvěma parametry, a to střední hodnotou (μ) (en. mean), která určuje polohu, a rozptylem (σ2) (en. variance), který je ukazatelem disperze.

Již jsme si řekli, že díky symetrii normálního rozdělení odpovídá jeho střední hodnota aritmetickému průměru, mediánu i modu, pokud hovoříme o celé populaci, tedy o parametrech. Potřebujeme-li střední hodnotu odhadnout pomocí statistiky vypočtené ze vzorku, je zdaleka nejpoužívanější statistikou aritmetický průměr (x̄) (en. sample mean).

S rozptylem se častěji setkáme ve formě směrodatné odchylky (σ – odmocnina z rozptylu, SD). Vzhledem k jejich jednoznačnému matematickému vztahu není nutné rozptyl a směrodatnou odchylku vnímat jako různé parametry, je však užitečné si uvědomit, že zatímco jednotky rozptylu odpovídají jednotkám veličiny umocněným na druhou, směrodatná odchylka vychází v jednotkách totožných se zkoumanou veličinou, což je právě důvodem k jejímu častému využití. Jednou z vlastností normálního rozdělení, která nám umožní představit interpretovat význam směrodatné odchylky, že v intervalu střední hodnota ± SD se nachází přibližně 68 % populace, v intervalu střední hodnota ± 2 SD cca 95 % a v intervalu střední hodnota ± 3 SD přibližně 99,7 % populace.

Význam výběrového rozptylu (s2) a výběrové směrodatné odchylky (s) je mezi uživateli často původcem zmatení. Rozdíl mezi rozptylem a směrodatnou odchylkou a jejich výběrovými protějšky je však prostý. Zatímco rozptyl a směrodatná odchylka a jsou parametry normálního rozdělení, tedy charakteristikami populace, výběrový rozptyl a výběrová směrodatná odchylka jsou statistiky, pomocí kterých odhadujeme hodnotu příslušných populačních parametrů s využitím vzorku.

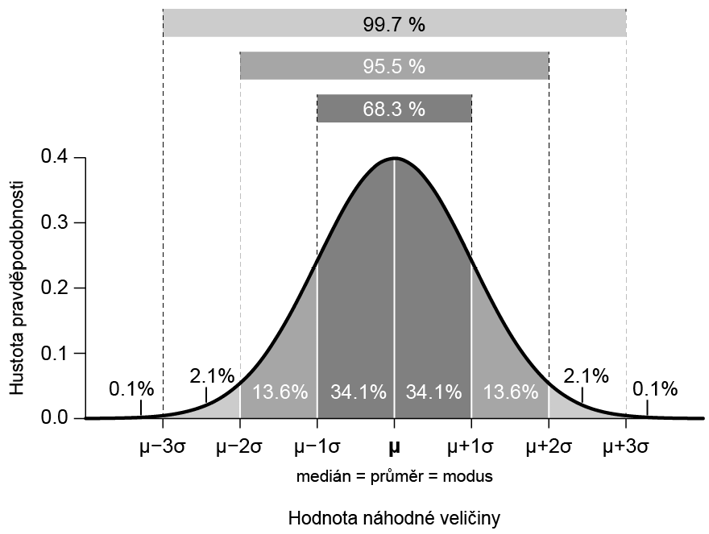
$Parametry normálního rozložení pravděpodobnosti C:\Users\hosek\Disk Google\_BC\OPVK\PART 1+2\Obrázky CZ\Normal distribution.png$

Obrázek 1: Parametry normálního rozdělení pravděpodobnosti

Statistikou normálního rozdělení, která nemá parametr obdobného významu, je střední chyba průměru (en. SEM – standard error of the mean). SEM se vypočítá vydělením výběrové směrodatné odchylky odmocninou z velikosti vzorku (počtu subjektů) a vystihuje spolehlivost, s jakou jsme se aritmetickým průměrem vypočítaným v našem vzorku přiblížili skutečné střední hodnotě veličiny v populaci. SEM proto často slouží jako výchozí hodnota pro přibližný výpočet intervalu spolehlivosti pro průměr (například interval arit. průměr vzorku ± 1,96 SEM obsahuje populační střední hodnotu s přibližně 95% spolehlivostí). Rozdíl mezi výběrovou směrodatnou odchylkou a střední chybou průměru spočívá tedy v tom, že zatímco výběrová směrodatná odchylka odhaduje, jak variabilní je hodnota veličiny u subjektů v populaci, střední chyba průměru udává přesnost odhadu střední hodnoty.

Tabulka 3: Shrnutí parametrů a statistik normálního rozdělení

Vlastnost	Statistika (ve vzorku)	Parametr (v populaci)
Poloha	aritmetický průměr (x̄) medián mode	střední hodnota (μ)
Disperze	výběrový rozptyl (s2)	rozptyl (σ2)
Disperze	výběrová směrodatná odchylka (s)	směrodatná odchylka (σ)
Spolehlivost odhadu střední hodnoty	střední chyba průměru (SEM)	-

Je nezbytné si uvědomit, že výběrový rozptyl, výběrová směrodatná odchylka a střední chyba průměru jsou statistiky příslušící výhradně normálnímu rozdělení a pro nenormálně rozdělené veličiny postrádá jejich hodnota smysl. To samé samozřejmě platí i pro parametry v populaci – směrodatnou odchylku a rozptyl – jiná rozdělení než normální takové parametry neznají.

Výběr statistik pro vyhodnocení a prezentaci dat

Pomocí vypočtené statistiky se zpravidla snažíme co nejpřesněji reprezentovat získaná experimentální data. Abychom byli v této snaze úspěšní, je nezbytné výběru statistiky věnovat náležitou pozornost.

Nejprve je ale vhodné zvážit, je-li výpočtu statistiky vůbec zapotřebí. Motivací výpočtu statistiky je totiž především redukce objemu dat pro prezentaci, kdy například průměrem a výběrovou směrodatnou odchylkou vypočtenými ze stovky měření tato měření shrneme do pouhých dvou hodnot. Máme-li však v našem vzorku měření jen hrstku, je na místě zvážit, zda je redukce nutná, když s sebou nevyhnutelně přináší nepřesnost (nezapomínejme, že statistiky jsou jen odhadem parametrů populace), a není-li v tomto případě vhodnější uvést (například vynést do grafu) samotné naměřené hodnoty.

Pojďme si nyní přiblížit nejčastější statistiky polohové:

•Aritmetický průměr (x̄) – Má největší význam u symetrických rozdělení, především u rozdělení normálního, kde je vhodným a nejčastěji používaným odhadem střední hodnoty. Pro výrazně nesymetrická rozdělení (v praxi tam, kde pozorujeme významně nenormální rozložení dat) však nelze aritmetický průměr doporučit jako univerzální polohovou statistiku. Hodnota aritmetického průměru však může být užitečná i v tomto případě, neboť vystihuje sumární efekt souboru – např. pokud je ve firmě o stech zaměstnancích průměrný plat 1100 EUR měsíčně, tak zároveň víme, že firma na mzdách měsíčně vyplatí 110000 EUR.

Problémem při použití aritmetického průměru je jeho citlivost vůči odlehlým pozorováním. Máme-li k dispozici dostatečně velký vzorek, můžeme nepříznivý vliv odlehlých hodnot omezit použitím ořezaného (en. trimmed mean) nebo winsorizovaného (en. winsorized) průměru namísto průměru aritmetického. Obě tyto metody spočívají v eliminaci či nahrazení stejného množství extrémních hodnot z obou okrajů rozdělení a následném výpočtu průměru aritmetického. Využití těchto metod je však stále vhodné jen u symetrických rozdělení, kde však dostatečně rozsáhlý vzorek (který je u těchto metod podmínkou) zpravidla umožňuje jako vhodný odhad střední hodnoty použít i medián.

•Medián – 0,5 kvantil. Hodnota veličiny, která dělí populaci na dvě stejné poloviny. Seřadíme-li subjekty podle hodnoty veličiny, je mediánem hodnota, která přísluší subjektu, jenž je přesně uprostřed (pokud je subjektů sudý počet, průměrujeme dva nejblíže středu).

Medián je vhodnou polohovou statistikou pro většinu rozdělení, největší význam má u rozdělení výrazně nesymetrických. Medián je také odolný vůči odlehlým pozorováním, nicméně je obtížně použitelný u extrémně malých vzorků.

•Modus – Hodnota s nejčetnějším výskytem (je-li statistikou) případně s nejvyšší hustotou pravděpodobnosti (je-li parametrem spojitého rozdělení). Jako polohová statistika u spojitých veličin měřených s dostatečnou přesností je zpravidla nevhodný, neboť většina naměřených hodnot je v tomto případě unikátní (pokud není vzorek v porovnání s přesností měření extrémně rozsáhlý). Často je však (mnohdy i nevědomě) používán pro diskrétní rozdělení s malým počtem hodnot.

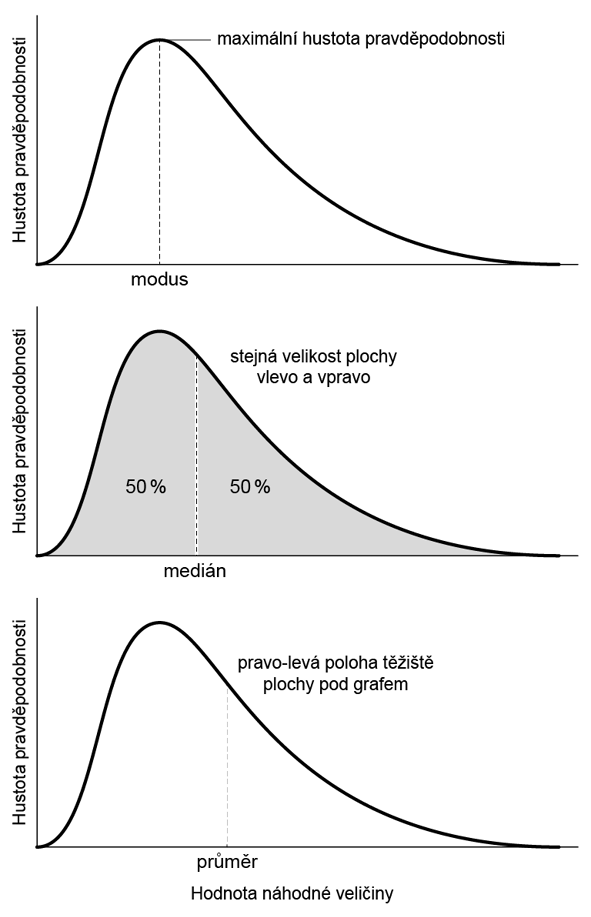
$Význam polohových statistik a jejich umístění u asymetrického rozdělení pravděpodobnosti C:\Users\hosek\Disk Google\_BC\OPVK\PART 1+2\Obrázky CZ\Location stats.png$

Obrázek 2: Význam polohových statistik a jejich umístění u asymetrického rozdělení pravděpodobnosti

a statistiky disperzní:

•Výběrový rozptyl, výběrová směrodatná odchylka – Jsou detailně popsány v předchozím oddílu. Náleží výhradně normálnímu rozdělení, pro jiné rozdělení nemají smysl.

•Kvartily, mezikvartilový rozptyl – Kvartily dělí populaci v poměru 25:75 (0,25 kvantil, dolní kvartil) a 75:25 (0,75 kvantil, horní kvartil). Jejich výpočet je analogický s výpočtem mediánu. Mezi kvartily se nachází 50 % subjektů. Mezikvartilové rozpětí, tedy rozdíl mezi hodnotou horního a dolního kvartilu, zpravidla uvádíme v textu a tabulkách, do grafu pak vynášíme samotné kvartily. Kvartily se hodí jednak všude tam, kde je vhodné použít medián, tedy u nesymetrických rozdělení, a jednak jsou i vhodné i pro symetrická nenormální rozdělení. Stejně jako medián však vyžadují rozumný počet pozorování v našem vzorku.

Předešlé vlastnosti statistik můžeme shrnout do jednoduchého návodu, s jehož pomocí můžeme snadno vybrat vhodnou polohovou a disperzní statistiku pro reprezentaci dat. Klíčovou otázkou je, má-li zkoumaná veličina normální rozdělení, což může být buď předem známo (např. z literatury), vyvozeno ze získaných dat, nebo předpokládáno.

Má zkoumaná veličina normální rozdělení a jsou data prosta odlehlých pozorování?

•ANO – Aritmetický průměr a směrodatná odchylka.

•NE nebo nevíme – Medián a kvartily.

POZOR, u velmi malých vzorků je platnost jakékoli vypočtené statistiky na pováženou.

Prezentace a vizualizace dat

I bez zprofanovaného úsloví, že „jeden obrázek vydá za tisíc slov,“ není zajisté třeba připomínat, že vizualizace dat je jedním z nejúčinnějších nástrojů pro prezentaci výsledků. Méně zřejmým faktem také je, že vhodné zobrazení dat, zvláště při složitějších experimentech, pomáhá i nám samotným se ve výsledcích orientovat a nacházet v nich zákonitosti, které by nám jinak mohly uniknout. Není proto moudré tuto fázi zpracování dat zanedbat a spokojit se s jakýmkoli grafem, který narychlo vytvoříme.

Vizualizace dat neoddělitelně obsahuje i složku estetickou, což nám při kombinaci s jasným a přehledným obsahem grafu či schématu umožní svoji práci mnohem lépe „prodat“. Toto tvrzení můžeme snadno demonstrovat na stoupající popularitě infografiky, tedy formy užitného grafického designu zaměřeného právě na prezentaci dat poutavou a kreativní grafickou formou srozumitelnou bez rozsáhlého komentáře. V odborné sféře se samozřejmě musíme s uměleckou invencí přiměřeně krotit, nicméně přehnaný ostych a slepé využívání několika zavedených typů grafů není rozhodně na místě, pokud objevíme přehlednější nebo snáze interpretovatelné zobrazení.

Vizualizace četnosti

S praktickými příklady vhodných grafů začneme u veličiny/statistiky, se kterou jsme v přehledu veličin skončili, tedy s četností.

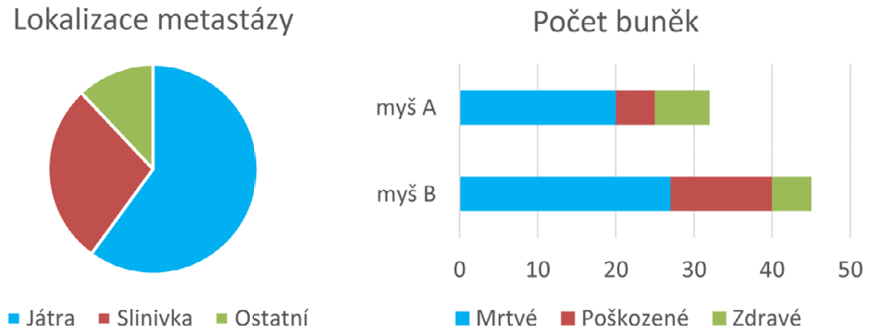
$Dva typické grafy pro znázornění četnosti - koláčový a pruhový C:\Users\hosek\Disk Google\_BC\OPVK\PART 1\Obrázky\koláč a pruh.png$

Obrázek 3: Dva typické grafy pro znázornění četnosti – koláčový a pruhový

Koláčový graf je vhodný pro zobrazení četnosti relativní, nicméně do každé výseče je možné vepsat i absolutní číselný údaj a poskytnout tak oba údaje naráz. Pruhový graf se naopak hodí pro zobrazení četnosti absolutní (přestože i pro četnost relativní je možné jej použít), kde nám jako bonus poskytne vizuální srovnání celkových počtů v jednotlivých skupinách. Toužíme-li i zde po vyjádření procentuálního zastoupení v jednotlivých skupinách, můžeme opět využít textového popisu v jednotlivých proužkových segmentech.

I zde se však dá uvažovat kreativně. Pokud například chceme využít koláčových grafů a zároveň porovnat celková množství ve skupinách, můžeme tento údaj promítnout do velikosti (průměru či plochy) koláče, čímž se dostáváme na pomezí symbolových grafů, o kterých bude podrobná řeč později [[Obr. 6; kapitola 4.3 Symbolové grafy]]. U pruhového grafu zase můžeme zobrazit hned dvě veličiny nebo dvě podskupiny naráz tak, že pro jednu budeme pruhy vynášet od nulové osy směrem doleva a pro druhou doprava. Vzhledem k tomu, že zrakem dovedeme poměrně přesně odhadnout střed úsečky, budeme z takového zobrazení schopni snadno porovnat velikost protilehlých pruhů.

Specifickým způsobem využití četností je kontingenční tabulka, kterou využíváme pro zkoumání vzájemné závislosti více (nejčastěji dvou) kategorických veličin (viz Tab. 4), tedy například jestli je mezi muži více kuřáků než mezi ženami. Hodnoty četností výskytu jednotlivých kombinací hodnot zkoumaných veličin se zapíší do příslušných buněk, jak je vidět na příkladu Tabulky 4.

Tabulka 4: Kontingenční tabulka

	Kouří	Nekouří
Muž	19	27	42
Žena	16	40	60
	35	67	102

V okrajových buňkách tabulky jsou zapsány součty sloupců a řádků, což nám poskytuje okamžitou informaci o četnosti v jednotlivých skupinách. U kontingenčních tabulek (ani u statistických testů, které z nich vycházejí) nezáleží na orientaci tabulky, tedy na tom, kterou veličinu zapíšeme do sloupců a kterou do řádků. Z informačního hlediska jsou oba způsoby rovnocenné. Největší výzvou při vizualizaci takové kontingenční tabulky je pak zachování „sčítání“ ve sloupcích i řádcích. V jednom směru totiž není problém použít na sebe naskládané sloupce či pruhy, které nám opticky součet znázorní, ale ve dvou směrech je situace složitější.

Nejčastěji využívanou možností jsou mozaikové grafy jako ten na Obr. 4.

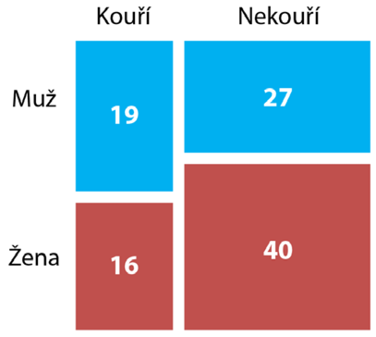
$Příklad nejčastěji využívaného grafu - mozaikového C:\Users\hosek\Disk Google\_BC\OPVK\PART 1\Obrázky\mosaic.png$

Obrázek 4: Příklad nejčastěji využívaného grafu – mozaikového

Mozaikový graf je sestrojen tak, že šířky jednotlivých obdélníků odpovídají souhrnným četnostem v příslušných sloupcích kontingenční tabulky (tedy v našem případě 35 kuřáků a 67 nekuřáků), obdélníky umístěné nad sebou jsou proto stejně široké a tvoří sloupce. Výšky obdélníků pak získáme tím, že celkovou výšku sloupce v grafu (tedy výšku grafu) rozdělíme v poměru jednotlivých buněk v odpovídajícím sloupci kontingenční tabulky (my jsme tedy vykreslili obdélníky v prvním sloupci s výškami v poměru 19:16). Graf zkonstruovaný tímto způsobem má tu důležitou vlastnost, že velikost plochy každého obdélníku odpovídá hodnotě v dané buňce kontingenční tabulky.

Výhodou mozaikových grafů je široká možnost jejich uplatnění. Je totiž možné je bez problémů použít pro kontingenční tabulky libovolných rozměrů, a dokonce i ve více dimenzích, tedy pro více než dvě kategorické proměnné zároveň. Způsob jejich konstrukce také zaručuje, že budou mít vždy podobu úhledného pravoúhelníku, který do dokumentu příjemně zapadne. K nevýhodám mozaikových grafů patří skutečnost, že v závislosti na uspořádání proměnných do řádků a sloupců kontingenční tabulky může výsledný graf vypadat různě (pro kontingenční tabulku se dvěma proměnnými můžeme dostat dvě různá uspořádání mozaikového grafu), nezachovávají si tedy výše zmíněnou vlastnost kontingenční tabulky, kde na uspořádání nezáleží. Pro čtenáře, který na tento typ grafu není zvyklý, také může zprvu obtížné se v něm zorientovat.

V nejjednodušším případě kontingenční tabulky velikosti 2x2 se můžeme některým nevýhodám mozaikových grafů vyhnout použitím zobrazení na Obr. 5.

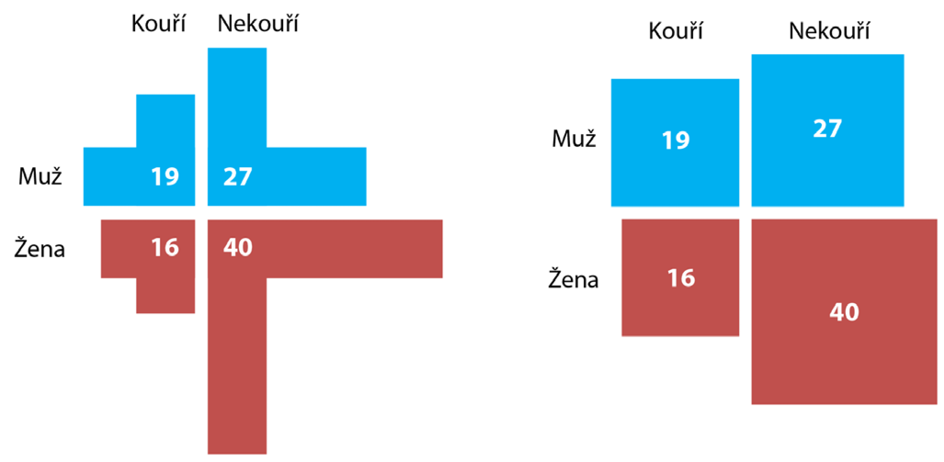
$Alternativní grafy pro kontingenční tabulku velikosti 2x2 C:\Users\hosek\Disk Google\_BC\OPVK\PART 1\Obrázky\multibar+square.png$

Obrázek 5: Alternativní grafy pro kontingenční tabulku velikosti 2x2

Na obrázku vlevo jsme pro zobrazení četností v jednotlivých buňkách použili sloupce a pruhy. Abychom zachovali možnost porovnání a aditivní charakter četností v řádcích i sloupcích, vykreslili jsme pro danou buňku vždy jeden sloupec (svislý segment) a jeden pruh (vodorovný segment), oba stejné velikosti odpovídající příslušné četnosti. Výhodou tohoto řešení je, že tak jako u sloupcových nebo pruhových grafů je příslušná hodnota vyjádřena délkou objektu, nikoli plochou, a je tedy snadné hodnotu porovnat a poměrně přesně odečíst (například pravítkem). Nevýhodu pak představuje prostorová náročnost takového zobrazení.

V grafu v pravé části obrázku jsou hodnoty příslušných buněk vyjádřeny plochou vykreslených čtverců. Výhodné v tomto případě je, že i při značných rozdílech četností v jednotlivých buňkách nezabere graf příliš místa, neboť při expanzi čtverce do výšky i do šířky jeho plocha rychle roste. Využití ploch, ačkoli je vizuálně poměrně snadno uchopitelné, představuje jistou nevýhodu, neboť z takového zobrazení není možné přesnou hodnotu snadno odečíst. Krom použití pravítka se tak nevyhneme umocňování (které nám zvýší chybu měření), stejně jako při konstrukci grafu je nezbytné využít odmocninu.

Oba popsané grafy jsou na rozdíl od grafu mozaikového symetrické vzhledem k řádkům a sloupcům, přistupují k nim tedy naprosto stejně a nezáleží, jak veličiny uspořádáme.

Alternativou k výše zmíněným typům grafů jsou i některé grafy tak trochu vypůjčené od kvantitativních veličin, k jejichž zobrazení se využívají nejčastěji (koneckonců jsme si už řekli, že četnost, i přes některé její výsady, můžeme považovat právě za kvantitativní veličinu). Mezi takové alternativy počítáme například grafy sloupcové, případně (zvláště pro rozsáhlé kontingenční tabulky) grafy symbolové, jak vidíme na Obr. 6.

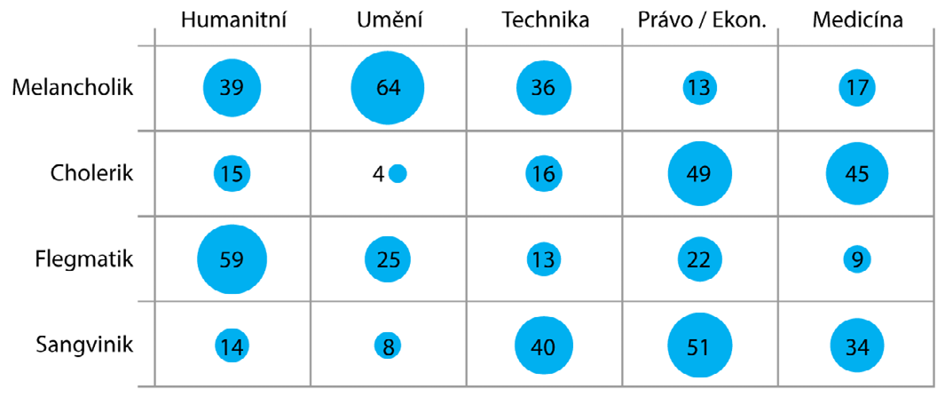
$Symbolový graf četnost v kontingenční tabulce C:\Users\hosek\Disk Google\_BC\OPVK\PART 1\Obrázky\crosstab circles.png$

Obrázek 6: Symbolový graf četností v kontingenční tabulce

Na rozdíl od ostatních kvantitativních veličit se při zobrazování četnosti nemusíme zabývat zobrazením odchylek, protože četnost ze své povahy definici žádného ukazatele variability neumožňuje.

Sloupcové grafy

Od tohoto okamžiku se budeme věnovat zobrazování kvantitativních veličin. V této oblasti pak nemůžeme začít jinde než u sloupcových grafů, tradičních evergreenů scény vizualizace dat. Sloupcové grafy používáme typicky pro zobrazení hodnoty jedné kvantitativní veličiny pro skupiny případů definované na základě jedné (to je snadné), dvou (to už tak snadné není) v nouzi nejvyšší i více kategorických proměnných (v tomto případě je však lepší hledat alternativní řešení). Je také možné zobrazit více kvantitativních veličin, když úměrně snížíme počet kategorií (pak je ale rozumné, aby veličiny měly stejné jednotky a mělo smysl je porovnávat).

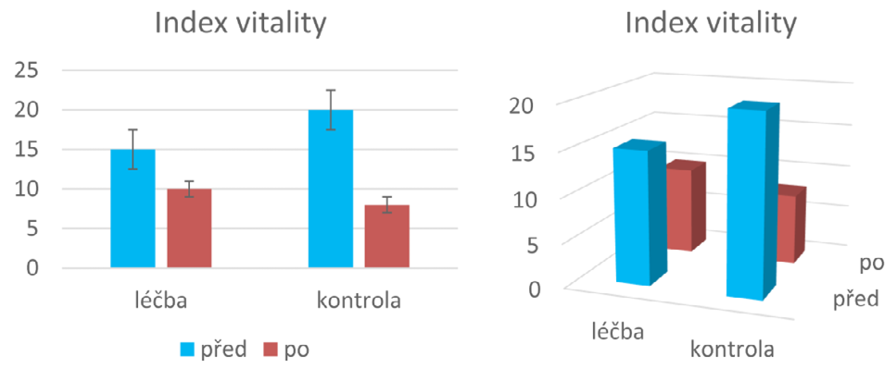
$Základní zobrazení sloupcového grafu C:\Users\hosek\Disk Google\_BC\OPVK\PART 1\Obrázky\sloupce.png$

Obrázek 7: Základní zobrazení sloupcového grafu

Při tvorbě sloupcového grafu pro více kategorií či veličin jsou nám k dispozici dva základní způsoby zobrazení. Prvním z nich (na obrázku 7 vlevo) je seskupování sloupců a druhým (vpravo) 3D zobrazení. Obě tyto varianty mají svá pro a proti. Seskupené sloupce jsou většinou obtížnější na orientaci, a pokud chce čtenář srovnávat grafy napříč skupinami, neubrání se patrně vícenásobnému studiu legendy a popisků. Na druhou stranu ale seskupené sloupce umožňují přesnější odečet výšky sloupce na svislé ose a je v nich také možné zobrazit úsečky odchylek. Do sloupců samotných je také možno vpisovat číselné údaje nebo popisky s vědomím, že budou viditelné a snadno čitelné. 3D zobrazení zpravidla umožňuje snáze srovnávat sloupce v obou „směrech“ kategorizace a nacházet v nich případné trendy. Nevýhodou této varianty je, že může být obtížné najít takové zobrazení, kde budou všechny sloupce viditelné (případně, máme-li grafů více, může být nutné každý z nich natočit jinak). V neposlední řadě není možné v 3D grafu znázornit úsečky odchylek a případné popisky se obtížně umisťují přímo do grafu. Je také třeba myslet na to, že nekvalitní tisk nebo fotokopie 3D grafu může být obtížněji čitelná.

Okénko pro hnidopichy: V praxi je často k vidění situace, kdy jsou ve sloupcovém grafu prezentována relativní data, tedy hodnoty veličiny v procentech vztažené k výšce jednoho ze sloupců (typicky ke kontrole), který má pak logicky výšku 100 %, případně 1. Takový sloupec pak již vlastně nenese žádnou informaci, nicméně může být prospěšný pro přehlednost zobrazení. Situace se však začíná komplikovat, chceme-li v takovém grafu zobrazit i směrodatné odchylky (případně jiné ukazatele variability měřené veličiny). Nejčastější postup spočívá ve vydělení hodnot ve všech sloupcích aritmetickým průměrem skupiny, ke které hodnoty vztahujeme. Sloupec, ke kterému jsme ostatní vztahovali, tak dosáhne hodnoty 1, přičemž si však zachová si svoji směrodatnou odchylku, jejíž měřítko se také přizpůsobí. Takový sloupec pak nese právě jen informaci o odchylce, neboť jeho jednotková výška je nevyhnutelná. Problém může nastat s interpretací odchylek sloupců ostatních, což můžeme demonstrovat následujícím příkladem:

Ve skupině kompenzovaných diabetiků a kontrolní skupině zdravých lidí jsme měřili glykémii. Hodnoty v obou veličinách vztáhneme k hodnotě dosažené kontrolní skupinou (často se pro tuto hodnotu používá nevhodné označení „kalibrátor“). Kontrolní skupina tedy vykazuje hodnotu 100 ± 10 % a skupina diabetiků 115 ± 26 % (uvádíme aritmetický průměr ± směrodatnou odchylku). Pokud tyto hodnoty vyneseme do sloupcového grafu, hrozí nebezpečí, že si čtenář vyloží druhý sloupec jako tvrzení: „Poměr glykémie u diabetiků a zdravých lidí je 1,15 ± 0,26.“ Tato interpretace však není správná, protože variabilita poměru diabetické a kontrolní skupiny závisí na odchylkách obou těchto veličin, zatímco my jsme pro druhý sloupec využili pouze odchylku diabetiků a odchylku kontrolní skupiny jsme ponechali na jejím sloupci, kde ji čtenář pravděpodobně přehlédne.

Řešení toho problému není snadné. Jsou-li totiž glykémie v obou skupinách normálně rozdělené, jejich poměr již normálně rozdělený není a směrodatnou odchylku tohoto poměru nemá smysl vyjadřovat (odvozená náhodná veličina má normální rozdělení, je-li součtem/rozdílem normálně rozdělených veličin, případně součinem/podílem log-normálně rozdělených veličin). Nezbývá tedy než se v případě přítomnosti směrodatných odchylek převodu na relativní hodnoty vyhýbat, případně čtenáře na problematickou interpretaci upozornit, je-li toto zobrazení nevyhnutelné. Toto se pochopitelně netýká jen směrodatných odchylek, ale i jiných ukazatelů variability veličin (SEM, mezikvartilové rozpětí, intervalové odhady apod.).

Symbolové grafy

Jsou-li naše data rozsáhlá, ať už co do počtu kategorií nebo kategorických veličin samotných, začne sloupcovým grafům brzy docházet dech, zobrazení začne být nepřehledné a orientace v něm složitá. V takovém případě nám někdy mohou pomoci symbolové grafy, které jsme již nakousli na konci kapitoly o kontingenčních tabulkách. Pod tímto nepěkným názvem máme na mysli grafy, ve kterých je hodnota kvantitativní veličiny znázorněna pomocí velikosti nějakého grafického symbolu, nejčastěji kruhu, obdélníku, čtverce apod. V případech, kde je originalita na místě, se však může jednat o panáčky, myšky nebo třeba prasátka. Podívejme se na příklad na Obr. 8.

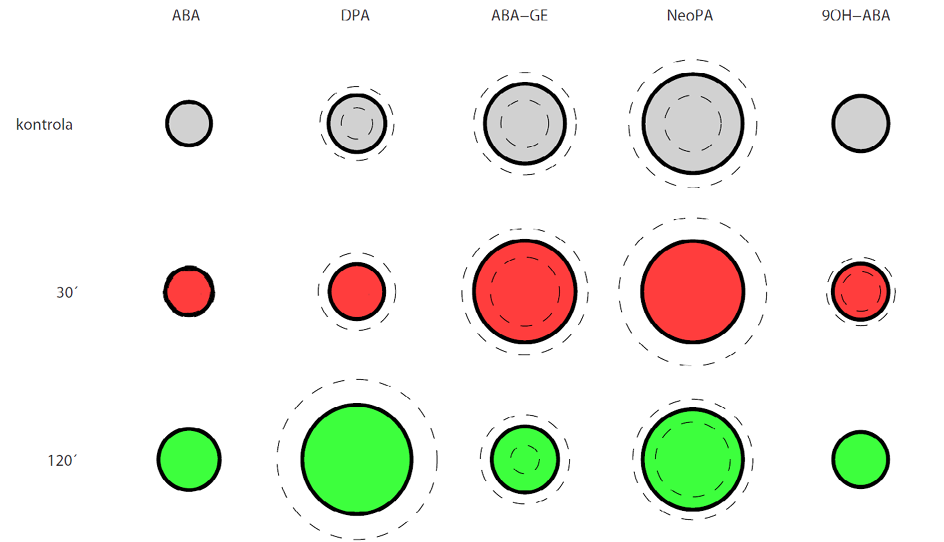
$Symbolový graf C:\Users\hosek\Disk Google\_BC\OPVK\PART 1\Obrázky\circles.png$

Obrázek 8: Symbolový graf

Hodnoty jedné kvantitativní veličiny jsou zde znázorněny pomocí velikosti kruhů uspořádaných do matice podle dvou kategorických proměnných. V případě potřeby bychom samozřejmě přímo do jednotlivých kroužků uvést i popisky s přesnou číselnou hodnotou. Přerušovanou čárou jsou vyznačeny kružnice odpovídající směrodatné odchylce zobrazené veličiny (přesněji řečeno odpovídají hodnotám průměr + směrodatná odchylka a průměr – směrodatná odchylka). Barevné označení výplně kruhů je v našem příkladu redundantní, slouží jen pro zdůraznění řádků, ale v případě potřeby můžeme barvu využít k vyznačení další relevantní informace (ať už kategorické proměnné nebo proměnné kvantitativní pomocí spojitého barevného spektra). Pro vyznačení jednoho binárního znaku (ano/ne – například statisticky významná odlišnost) můžeme využít obrysovou čáru příslušného kruhu, kterou buďto zobrazíme, nebo ne. Nevětší přednost tohoto zobrazení ale spočívá ve snadném porovnání zobrazené kvantity podle obou kategorických proměnných (tedy jak v řádcích, tak sloupcích), a to i v případě opravdu velkého počtu kategorií. Nevýhodou naopak je, že na rozdíl od sloupců není pomocí symbolů možné zobrazit záporné hodnoty.

V případě symbolů je nejdůležitější definovat, jaké měřítko jejich velikosti bude reprezentovat příslušnou hodnotu – zda to bude jejich plocha nebo vhodný délkový parametr (průměr kruhu, délka hrany čtverce, výška panáčka apod.). Rozhodnutí je v tomto případě na nás a závisí na okolnostech – zobrazení pomocí ploch pomůže snížit prostorové nároky pro zobrazení u veličin s vysokým rozsahem hodnot a je vizuálně poměrně intuitivně vnímáno (všichni přece víme, že koláč nebo pizza dvojnásobného průměru je čtyřikrát větší). Zobrazení pomocí délkového měřítka naopak rozdíly mezi hodnotami zvýrazňuje (čehož bývá někdy zneužíváno například v reklamě) a umožňuje snadnější odečet hodnot.

Krabicové grafy

Doposud jsme při zobrazení kvantitativní veličiny řešili, kolik kategorií nebo veličin je možné pomocí daného typu grafu zobrazit, přičemž jsme se spokojili se zobrazením střední hodnoty a jednoho ukazatele variability (nejčastěji směrodatné odchylky). Tato zjednodušená reprezentace rozdělení veličiny však (zejména u nenormálně rozdělených veličin) často nestačí, a proto se nyní zaměříme právě na podrobnější zobrazení tvaru rozdělení měřené veličiny.

Nejčastěji bývá k tomu to účelu využíván krabicový graf jako ten na Obr. 9.

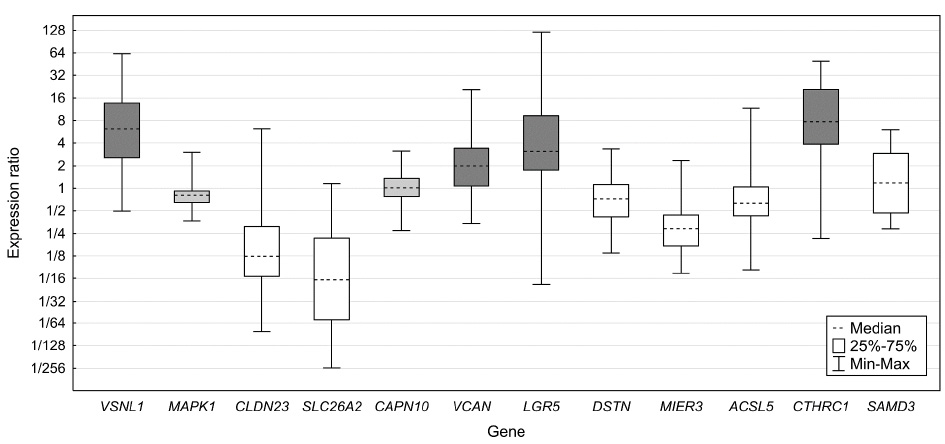
Ukázka krabicového grafu

Obrázek 9: Ukázka krabicového grafu

Přerušovanou čarou je vyznačen odhad střední hodnoty (medián), krabice samotná označuje mezikvartilové rozpětí a úsečky vyznačují minimální a maximální hodnotu. V závislosti na našich potřebách však můžeme v krabicovém grafu zobrazit jakékoli smysluplné statistiky (aritmetický / geometrický / kvadratický průměr, modus, směrodatnou odchylku, SEM, intervaly spolehlivosti atd.), nicméně použití kvantilů (tj. právě mediánu a kvartilů) je nejčastější, protože u normálně rozdělených veličin, kde je možné použít směrodatnou odchylku, směrodatná odchylka k popisu variability veličiny dostačuje a krabicového grafu není zapotřebí. Je možné se setkat také se zobrazením minima a maxima bez odlehlých měření pomocí úseček s následným vyznačením těchto pozorování vhodnou značkou (např. hvězdičkou). Za zmínku stojí i možnost využití logaritmické osy (což platí pro všechny typy grafů), která je v uvedeném příkladu vizualizace expresních dat zcela namístě (odpovídá exponenciálnímu charakteru dat).

Histogram

Ještě dál můžeme při zobrazení rozdělení veličin zajít s využitím histogramu. Pro konstrukci histogramu je nejprve interval zjištěných hodnot kvantitativní veličiny rozdělen na vhodný počet navazujících podintervalů a spočteny četnosti hodnot do těchto podintervalů spadajících. Tyto četnosti jsou následně zobrazeny v grafu jako sloupce. Na rozdíl od sloupcového grafu, kde jsou mezi sloupci mezery, na sebe sloupce histogramu přímo navazují. Vhodně zkonstruovaný histogram představuje odhad rozdělení pravděpodobnosti měřené veličiny ve statistickém vzorku a je-li použitý vzorek reprezentativní, tak také ve zkoumané populaci. Ukázku histogramu vidíme na Obr. 10.

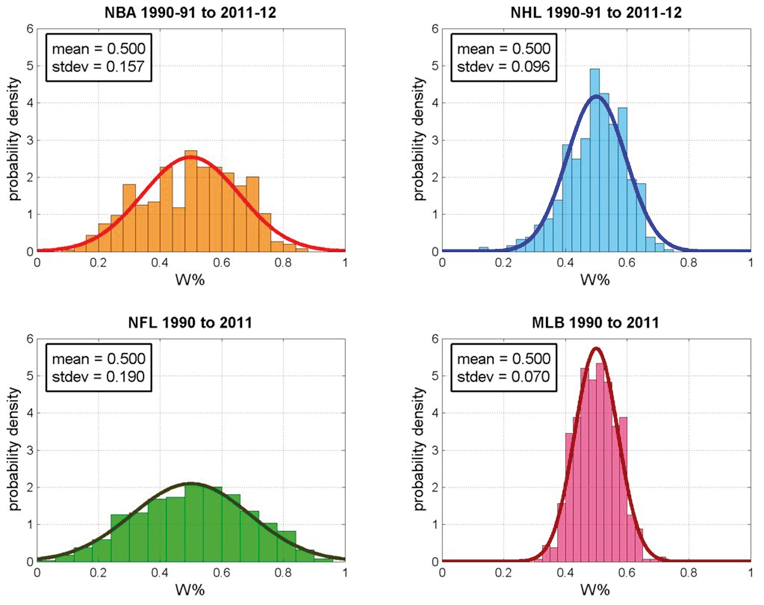
Ukázka histogramů

Obrázek 10: Ukázka histogramů (převzato z http://pts-in-the-paint.blogspot.cz)

Jedná se o histogramy veličiny udávající relativní počet výher týmů v nejvyšších amerických soutěžích v basketbalu, hokeji, americkém fotbalu a baseballu. Širší a nižší histogram znamená, že v dané soutěži panují mezi jednotlivými týmy větší rozdíly, tedy existují trvale dominující týmy a týmy s nízkou výkonností. Úzký a vysoký graf naopak značí vyrovnanost soutěže.

Ale zpět k histogramům jako takovým. V ukázce vidíme, že samotné sloupce histogramu jsou doplněny o zobrazení normálního rozdělení nejvíce podobného získanému histogramu. Jedná se o poměrně častý způsob, jak vizuálně odhadnout, je-li rozdělení zkoumané veličiny normální či nikoli, což je otázka poměrně zásadní (a ještě si o ní mnohé povíme). Zobrazení histogramu naměřených hodnot je tak často prvním krokem analýzy dat, byť slouží často jen pro určení dalšího postupu zpracování a málokdy je získaný histogram publikován.

Je-li náš vzorek dostatečně rozsáhlý (tedy máme-li dostatek změřených hodnot pro naplnění jednotlivých podintervalů), poskytuje nám histogram nejpřesnější pohled na rozdělení naší veličiny. Když ale přijde na srovnání hodnot veličiny mezi skupinami, s čímž předchozí typy grafů neměly problém, jsou možnosti histogramu omezené. U dvou skupin (více není kvůli přehlednosti rozumné) je možné vykreslit histogramy přes sebe či zrcadlově proti sobě (jeden nahoru, druhý dolů, případně vodorovně vlevo / vpravo), pro více skupin pak nezbývá, než použít několik oddělených grafů, což nám ovšem porovnání drobných rozdílů komplikuje. Na Obr. 11 uvádíme příklad překrývajících se histogramů.

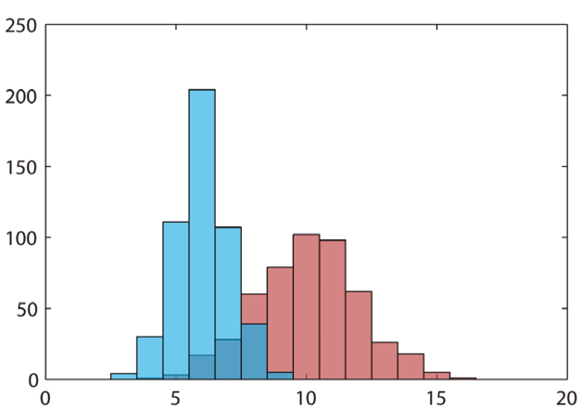
$Příklady překrývajících se histogramů C:\Users\hosek\Disk Google\_BC\OPVK\PART 1\Obrázky\double histogram.png$

Obrázek 11: Příklad překrývajících se histogramů

Okénko pro fotografy: Pro úplnost můžeme v rámci drobné odbočky uvést, že s histogramem se často setkáme i při editaci digitálního obrazu, zejména fotografií. Histogram nám v tomto případě udává rozdělení jasu v obrazu, tedy počty pixelů s danou hodnotou (nebo intervalem hodnot) jasu, a to buď celkového, nebo v jednotlivých barevných kanálech (červená, zelená, modrá). Z histogramu obrazu můžeme vyčíst, jak vysoký je kontrast obrazu, jak dalece je využit dostupný dynamický rozsah (například nedochází-li při expozici k tzv. přepalům nebo podpalům) nebo odhadnout kvalitu vyvážení bílé, fotografujeme-li na barevně neutrálním pozadí.

Hroznový graf

Potřebujeme-li co nejpřesněji vizualizovat rozdělení změřené veličiny a zároveň porovnat větší množství kategorií, bývá často výhodné použít hroznový graf (nebo také „včelí roj“ z angl. beeswarm plot). Tento typ grafu můžeme považovat za velmi schopného křížence histogramu a krabicového grafu.

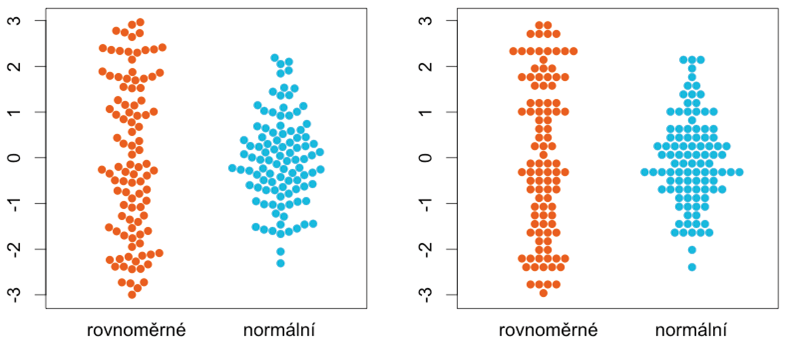
Příklady hroznového grafu pro 2 kategorie: V jedné z nich jsou hodnoty rozdělené rovnoměrně, v druhé normálně.

Obrázek 12: Příklad hroznového grafu pro dvě kategorie. V jedné z nich jsou hodnoty rozdělené rovnoměrně, v druhé normálně

Každá tečka reprezentuje jednu naměřenou hodnotu (například jednoho pacienta, pokusné zvíře apod.), které přibližně odpovídá její svislá pozice. Vodorovně jsou pak tečky uspořádány co nejblíže ose roje tak, aby se nepřekrývaly. Graf vlevo a vpravo se liší způsobem, jak jsou tečky umisťovány (existuje jich ještě více), ale princip zobrazení je totožný. V hroznovém grafu můžeme vyznačit i odhad střední hodnoty pomocí vodorovné čáry.

Největší výhodou hroznových grafů je skutečnost, že nezobrazujeme statistiky z dat vypočtené, ale data samotná. Vyhýbáme se tak nebezpečí, že zvolená statistika nebude povahu dat vhodně vystihovat nebo bude zavádějící. Tato vlastnost je užitečná zejména v případech, kdy se potýkáme s malými vzorky, u nichž je určení rozdělení měřené veličiny a výpočet vhodné statistiky problematické. V souladu se zásadou zmíněnou v první kapitole je potom nejjednodušší nechat „mluvit“ data samotná a neprovádět více statistiky, než je nutné.

Bodové grafy (scatter plots)

Dosud jsme se věnovali zobrazení hodnoty nebo rozdělení hodnot kvantitativních veličin, a to zpravidla v několika kategoriích. Často se však setkáme i se situací, kdy budeme potřebovat znázornit souvislost dvou kvantitativních veličin mezi sebou (například že lidé vyššího vzrůstu mají většinou vyšší tělesnou hmotnost). Krom možnosti kategorizace jedné nebo obou proměnných do intervalů a využití předchozích typů grafů, což zpravidla nebývá nejvhodnější, jsou nám v tomto případě k dispozici bodové grafy, anglicky scatter plots.

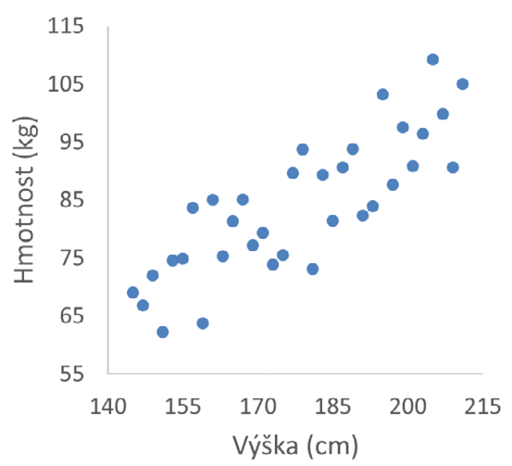
$Ukázka bodového grafu C:\Users\hosek\Disk Google\_BC\OPVK\PART 1\Obrázky\scatterplot.png$

Obrázek 13: Ukázka bodového grafu

V bodovém grafu (viz příklad na Obr. 13 ilustrující právě závislost hmotnosti na tělesném vzrůstu) představuje každý bod jeden případ (opět jeden subjekt z našeho vzorku, tedy jednoho pacienta, zvíře apod.), přičemž jeho vodorovná a svislá poloha odpovídá dvojici hodnot zkoumaných veličin změřených pro příslušný subjekt (zde tedy po řadě výšce a hmotnosti). Z tvaru výsledného „obláčku“ bodů můžeme snadno posoudit, zda mezi veličinami souvislost existuje či nikoli. Pokud máme představu o tvaru závislosti, která by se v datech měla nacházet, bývá bodový graf často proložen příslušnou křivkou.

Závislost mezi kvantitativními veličinami však není jediným vztahem mezi nimi, který můžeme chtít zobrazit. Může být například zapotřebí vizualizovat nějakou komplexní vlastnost jednotlivých subjektů vzorku, která bude určena více faktory (změřenými kvantitativními veličinami). Dejme tomu výhodnost nákupu automobilu je ovlivněna řadou faktorů, z nichž můžeme vybrat třeba pořizovací cenu a provozní náklady na ujetý kilometr. Zakreslíme-li dostupné vozy do bodového grafu, budou nejvýhodnější ty nejblíže počátku soustavy souřadnic. Vozy vzdálené od počátku jsou naopak výhodné nejméně. Podobným způsobem můžeme ověřit, je-li míra šílenosti potenciálního sexuálního partnera/partnerky akceptovatelná s ohledem na jeho/její atraktivitu pomocí sexy/blázen stupnice na Obr. 14 (Stinson B., Parťákodex, 2010).

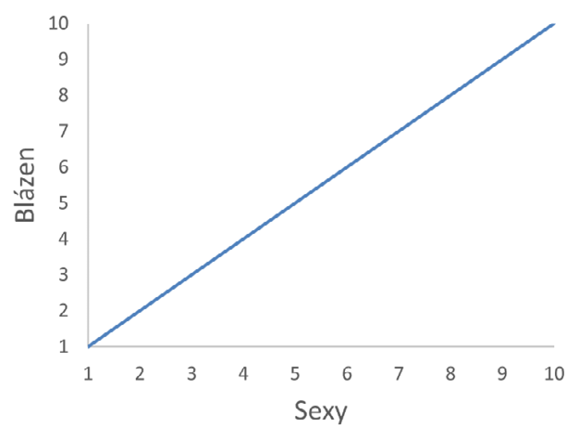
$Bodový graf pro posouzení dvou kvantitavních vlastností jednoho subjektu. C:\Users\hosek\Disk Google\_BC\OPVK\PART 1\Obrázky\Sexy - blázen.png$

Obrázek 14: Bodový graf pro posouzení dvou kvantitativních vlastností jednoho subjektu

Pomocí definovaných kritérií přidělíme studované osobě hodnoty veličin „Sexy“ a „Blázen“ na stupnici od 1 do 10 a zakreslíme bod na příslušné souřadnice v grafu. Nachází-li se bod pod osou prvního kvadrantu (přímkou sexuálně akceptovatelného šílenství, znázorněnou modře), je riziko přípustné. Bod nad osou kvadrantu je naopak varovným signálem a startovním výstřelem k rychlému ústupu.

Grafy více než dvou kvantitativních veličin

Vzroste-li počet kvantitativních veličin na tři a více, začínají se možnosti komplikovat. Bodové grafy je sice teoreticky možné rozšiřovat do dalších dimenzí prakticky bez omezení, nicméně dvojrozměrné prezentační médium (papír, displej počítače) a maximálně trojrozměrná pravoúhlá soustava souřadnic, kterou jsme schopni v dimenzích našeho světa zkonstruovat, nás v tomto případě velmi omezují. Jako myšlenkový konstrukt je však představa vícerozměrných dat jako množiny bodů v prostoru, kde každá z nezávislých souřadnic představuje hodnotu jedné veličiny, velmi užitečná.

Je-li však zkoumaných případů rozumně nízký počet a měřené veličiny jsou společnými faktory jedné vlastnosti, kterou se snažíme vizualizovat, můžeme využít grafu paprskového (angl. radar plot).

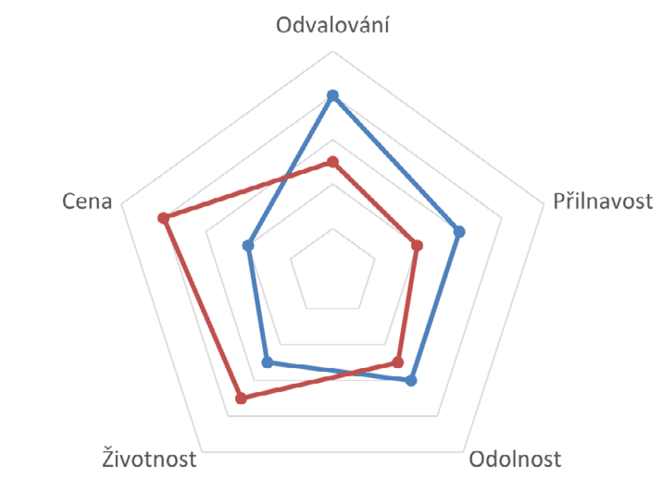
$Ukázka paprskového grafu C:\Users\hosek\Disk Google\_BC\OPVK\PART 1\Obrázky\paprsky.png$

Obrázek 15: Ukázka paprskového grafu

Na Obr. 15 vidíme příklad paprskového grafu srovnávající ho dva modely veloplášťů. Na rozdíl od Stinsonovy sexy/blázen stupnice z předchozí části je nutné, aby všechny veličiny vynášené do paprskového grafu měly na výslednou vlastnost shodný účinek, tedy aby vždy pro všechny platilo buď „čím víc, tím líp“, nebo opačně. Faktory, které mají opačný smysl než většina ostatních, musíme vhodným způsobem převést (například místo ceny uvést úsporu oproti nejdražšímu modelu nebo místo spotřeby pohonných hmot použít dojezd na jeden litr). Proměnné také nesmí nabývat záporných hodnot, které bychom nebyli schopni znázornit. Aby bylo výsledné zobrazení reprezentativní, je navíc většinou nutné standardizovat rozsah veličin do vhodné stupnice (1–10, pořadí mezi testovanými subjekty, procenta apod.). Takové zobrazení nám umožňuje porovnat jak konkrétní vlastnosti zobrazených případů, tak odhadnout jejich celkovou kvalitu podle plochy zobrazených mnohoúhelníků.

Zobrazení posloupností

Posledním způsobem vizualizace dat, na který si posvítíme, je znázornění posloupností, například časového sledu měření určité veličiny, který vidíme na Obr. 16.

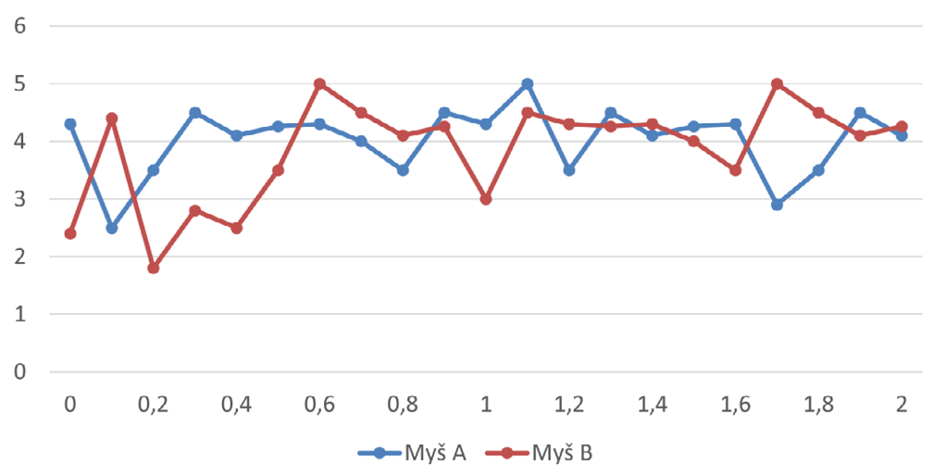
$Grafické znázornění posloupností C:\Users\hosek\Disk Google\_BC\OPVK\PART 1\Obrázky\řada.png$

Obrázek 16: Grafické znázornění posloupností

Toto zobrazení je asi tou nejtypičtější představou, která se nám pod slovem graf vybaví. Jednotlivé body reprezentují zjištěnou hodnotu veličiny v příslušném čase, pokud bylo měření opakované nebo zobrazujeme výsledky celé skupiny případů jako jednu řadu, může se jednat i o vhodnou statistiku (např. aritmetický průměr), eventuálně doplněnou měřítkem variability (např. směrodatnou odchylkou) znázorněnou úsečkami okolo bodů. Dalšími vlastnostmi tohoto typu grafu, kterým se můžeme věnovat, jsou výběr vhodného měřítka os (linární/logaritmické) a možnost zobrazení dvou svislých os (například ve dvou různých jednotkách nebo jednu pro absolutní a druhou pro relativní vyjádření).

Důležitou součástí grafů posloupností jsou křivky spojující jednotlivé body. Jejich primární úlohou je vizuální propojení bodů dané řady, což nám výrazně usnadňuje orientaci v grafu. Krom této vlastnosti nám také mohou pomoci odhadnout, jak se hodnota veličiny vyvíjela mezi měřeními (tento proces nazýváme interpolace). Ať už použijeme jakýkoli z početných způsobů interpolace (prosté úsečky mezi body nebo hladké propojení – např. kubický spline), nesmíme zapomínat, že se jedná jen o odhad a z hlediska dat žádnou informaci o hodnotě mezi měřeními nemáme.

Testování hypotéz

Principy testování

Základním aparátem pro aplikaci principu statistické indukce je testování hypotéz, které nám umožnuje z hlediska pravděpodobnosti posoudit, jak dalece odpovídají data zjištěná v našem vzorku hypotetickým vlastnostem populace. V zásadě jsou proti sobě postaveny vždy dvě hypotézy – nulová (H0) a alternativní (H1). Tyto hypotézy (a v návaznosti na ně i testy) mohou být oboustranné nebo jednostranné.

U oboustranného testu, který je využíván ve valné většině případů, vyjadřuje nulová hypotéza předpoklad nulového rozdílu či nezávislosti veličin (např. průměrný věk mužů a žen se neliší, neexistuje souvislost mezi krevním tlakem rizikem infarktu myokardu) Druhá, tzv. alternativní hypotéza, je pak logickou negací hypotézy nulové a představuje zpravidla závěr, který chceme v datech prokázat (statisticky významný rozdíl, závislost veličin). Testy jednostranné pracují hypotézami tvořenými dvěma doplňkovými jednostrannými intervaly (H0: průměrný úbytek váhy po užití preparátu je větší než nula - tedy v intervalu (0, ∞); H1: průměrný úbytek váhy je menší nebo roven nule - v intervalu (-∞, 0˃).

Princip testování hypotéz je poměrně prostý. Nejprve si musíme uvědomit, že i když nulová hypotéza v populaci platí, tak data zjištěná v našem vzorku jí nemusí zcela odpovídat. Například zcela férový hod mincí skýtá přesně stejnou pravděpodobnost, že padne panna i orel, což je naše nulová hypotéza. Provedeme-li deset hodů (což bude náš vzorek), máme i přes to jen cca 25% šanci, že padne pětkrát panna a pětkrát orel. S největší pravděpodobností tedy dostaneme výsledek, který se s nulovou hypotézou neshoduje.

Principem testů hypotéz je stanovení, v jak silném rozporu s nulovou hypotézou je výsledek pozorovaný v našem vzorku. Toho dosáhneme, určíme-li pravděpodobnost, se kterou při platnosti nulové hypotézy můžeme získat stejné nebo ještě více se odchylující výsledky. Pokud by výsledkem našeho pokusu s mincí bylo sedm panen a tři orli, sečetli bychom tedy pravděpodobnosti výsledků 7:3, 8:2, 9:1, 10:0 a pro oboustranný test také 3:7, 2:8, 1:9 a 0:10. Výsledkem je v tomto případě 0,34, tedy i v případě dokonale férové mince máme 34% šanci získat výsledek 7:3 nebo extrémnější. Tato pravděpodobnost se označuje jako p-hodnota a je tím větší, čím lépe získaná data odpovídají nulové hypotéze.

V případě naší mince dojdeme vcelku jasně k závěru, že experimentální výsledek s 34% šancí výskytu není v přílišném rozporu s nulovou hypotézou a nenabydeme přesvědčení, že mince je mince zmanipulovaná, tedy nezamítneme nulovou hypotézu. Co bychom ale dělali v případě, kdyby výsledná p-hodnota byla 0,15, 0,1, 0,05 nebo 0,01? Zvykem je předem určit prahovou hodnotu p-hodnoty, pod kterou již budeme výsledky považovat za příliš zvláštní, než aby nulová hypotéza platila, a budeme ji zamítat. Tuto hodnotu označujeme α a nazýváme ji hladinou významnosti testu. Obvyklou (často i zcela slepě aplikovanou) hodnotou hladiny významnosti je 0,05, ale můžeme se setkat i s hodnotou 0,01 a dalšími. Po výpočtu p-hodnoty ji tedy srovnáme s hladinou významnosti α a postupujeme následovně:

•Je-li p≥α, data neprokázala dostatečný rozpor s nulovou hypotézou a tu proto nezamítáme. Často bývá v tomto případě uváděno, že nulovou hypotézu přijímáme, nicméně tato formulace je krajně nevhodná, neboť nezamítnutí nulové hypotézy její platnost rozhodně nepotvrzuje.

•Je-li p<α, našli jsme dostatek důkazů pro zamítnutí nulové hypotézy, a proto přijímáme alternativní hypotézu o rozdílu.

Chyby, síla a spolehlivost testů

Vzhledem k pravděpodobnostnímu charakteru výsledku testu je zřejmé, že jeho výsledek nemusí být pravdivý, tedy že se při jeho vyslovení dopustíme chyby (viz tabulka 4). Statistické chyby rozlišujeme na chybu I. druhu (falešně pozitivní výsledek – zamítneme H0, přestože platí – tedy nalezneme rozdíl či závislost, která ve skutečnosti neexistuje) a chybu II. druhu (falešně negativní výsledek – nezamítneme H0, přestože neplatí – nenalezneme rozdíl či závislost tam, kde ve skutečnosti je).

Pravděpodobnost, že se dopustíme chyby prvního druhu, je rovna hladině významnosti testu (α). Naopak s doplňkovou pravděpodobností 1-α je zamítnutí nulové hypotézy v souladu s realitou, a tato pravděpodobnost proto udává hladinu spolehlivosti (en. level of confidence) testu. Pravděpodobnost chyby druhého druhu označujeme β a odvozujeme z ní i tzv. sílu testu kterou vypočteme jako 1-β. Síla testu udává pravděpodobnost, že skutečný efekt přítomný v populaci bude pomocí testování našeho vzorku odhalen. Pravděpodobnosti α a β spolu úzce souvisí – snížíme-li hodnotu hladiny významnosti α, dojde nevyhnutelně ke zvýšení hodnoty β a naopak. Přesná závislost těchto hodnot však závisí na konkrétním testu, velikosti vzorku a velikosti efektu, který se snažíme v datech odhalit, a hodnotu β proto není možné určit z hodnoty α jednoduchým výpočtem.

Pravděpodobnost chyby II. druhu se pokoušíme odhadnout především při plánování experimentu, k čemuž slouží analýza síly testu. Zpravidla akceptujeme sílu testu přibližně 0,8 a více, připouštíme tedy vyšší pravděpodobnost chyby II. druhu (hodnoty β až 0,2) než u chyby I. druhu (obvykle 0,05), jsme tedy opatrnější vůči falešně významnému výsledku, než vůči neobjevení existující závislosti. Z hlediska plánování experimentu odpovídá α pravděpodobnosti, že zjistíme nepravdivý významný výsledek, zatímco β je pravděpodobnost, že vynaložíme prostředky na experiment, aniž bychom existující závislost objevili.

Tabulka 5: Rozhodnutí a chyby při testování hypotéz

Realita		Výsledek testu
		H0 zamítnuta (signifikantní výsledek)	H0 nezamítnuta (nesignifikantní výsledek)
	H0 platí (nemá být zmítnuta)	Chyba I. druhu hladina významnosti α	OK hladina významnosti 1 - α
	H0 platí (H má být zamítnuta)	OK síla testu 1 - β	Chyba II. druhu β

Síla testu má zásadní význam i při interpretaci negativních výsledků, tedy situace, kdy test v datech neprokáže významný efekt. Vzhledem k tomu, že síla testu je zpravidla menší než hladina spolehlivosti (neboli β>α) a že přesná hodnota síly testu je zpravidla neznámá, není v takovém případě možné bez dalšího zkoumání prohlásit nulovou hypotézu za platnou, tedy prohlásit, že se v populaci hledaný efekt nevyskytuje. Sílu testu je sice teoreticky možné vypočítat i během analýzy již naměřených dat, nicméně post-hoc výpočet síly testu není korektní a je vhodnější negativní výsledky interpretovat prostřednictvím intervalových odhadů a dalších nástrojů (Hoenig a Heisey, 2001).

Již jsme zmínili, že do vztahu mezi hodnotami α a β vstupuje také velikost vzorku a rozsah hledaného rozdílu či efektu. Čím je náš vzorek větší (co do rozsahu, počtu pacientů), tím menší rozdíly zkoumaného parametru stačí k tomu, abychom zamítli nulovou hypotézu o shodě. Tento vztah můžeme formulovat i opačně, a sice že k prokázání malého rozdílu mezi skupinami potřebujeme rozsáhlý vzorek.

Při interpretaci výsledků testů je také nutné rozlišovat mezi termíny „statistická významnost“ a „klinická významnost“. Vrátíme se nyní k příkladu s mincí a představíme si, že padla devětkrát panna a jednou orel. V tomto případě je p-hodnota přibližně 0,02 a my tak na standardní hladině významnosti 0,05 zamítáme nulovou hypotézu a tvrdíme, že mince je zaujatá ve prospěch výsledku panna. V žádném případě to ale neznamená, že by padaly jenom panny, ani že by byla šance na pannu devětkrát vyšší než na orla. Podobně i v případě, kdy například prokážeme, že muži mají významně vyšší tělesnou hmotnost než ženy (což můžeme předpokládat), se jedná jen o tendenci určitého omezeného rozsahu, neboli o rozdíl ve střední hodnotě veličiny, nikoli o univerzální pravidlo. Stále budou existovat muži s nižší hmotností než některé ženy a naopak, takže jen podle tělesné hmotnosti bychom nejspíš pohlaví příliš spolehlivě uhodnout nedokázali. Stejně tak i v dalších případech, kdy dojde k zamítnutí nulové hypotézy o shodě, může být rozdíl tak malý, že pro klinickou praxi je tento rozdíl zcela nevýznamný. Je-li naším cílem použít nalezený statisticky významný rozdíl jako diagnostický ukazatel, můžeme kvalitu takového ukazatele vyhodnotit pomocí plochy pod ROC křivkou.

Volba jednostranného či oboustranného testu (en. one-tailed vs. two-tailed)

Protože jednostranný test poskytuje větší sílu než test oboustranný (máme větší šanci prokázat signifikantní rozdíl), můžeme se ocitnout v pokušení využívat především jednostranné varianty testů. Použití jednostranného testu je však možné pouze tehdy, máme-li dostatečný důvod se věnovat pouze jednostrannému srovnání ještě před pohledem do dat – v žádném případě možné volit jednostranný test až podle tendence vypozorované v datech. Pokud tedy například experimentální skupina vykazuje zvýšení hodnot oproti skupině kontrolní, nemůžeme v žádném postupovat na základě úvahy „výsledky vykazují vyšší hodnotu, chceme tedy zjistit, zda je opravdu vyšší (nižší nás nezajímá, protože jsme naměřili vyšší) a proto použijeme jednostranný test“. V tomto případě je třeba si vzpomenout, že testy významnosti vyhodnocují pravděpodobnost získaného výsledku za předpokladu, že se skupiny neliší. Proto v případě, že pozorovaný rozdíl pozorujeme pouze náhodou, mohl být se stejnou pravděpodobností i opačný. Stručně tedy můžeme říci, že chceme-li pouze zjistit, zda je efekt (rozdíl nebo závislost veličin) pozorovaný v datech statisticky významný, používáme výhradně testy oboustranné.

I v případě, kdy máme předem představu o směru efektu (tedy očekáváme-li zvýšení či snížení, případně kladnou či zápornou závislost), však není použití jednostranného testu bez rizika. Může totiž dojít k situaci, kdy data budou jednoznačně vypovídat o efektu opačném, který však jednostranný test zaměřený na původně předpokládaný směr efektu odhalit nedokáže. Pokud bychom se tedy například snažili prokázat vyšší účinnost nového léčiva v porovnání s léčivem zavedeným pomocí jednostranného testu, nemáme šanci tímto testem odhalit, zda není účinnost nového léčiva nižší. Použití jednostranného testu je proto možné pouze v případě, že neodhalení opačného efektu nezpůsobí výrazné problémy či škody. Testujeme-li například levnější alternativu léčiva, můžeme jednostranný test použít, abychom prokázali, že není méně účinný než léčivo stávající. Test v tomto případě sice nedokáže odhalit, zda není účinnost nového léčiva vyšší, což ovšem není na závadu, neboť nebude-li horší, bude nové léčivo pravděpodobně nasazeno tak jako tak.

Problém vícenásobného testování

Je nezbytné si uvědomit, že pravděpodobnost chyby I. druhu (α) platí pro každý test zvlášť, a provedeme-li testů více, pravděpodobnost, že dostaneme alespoň jeden falešně pozitivní výsledek, roste. Například pro 5 testů je tato pravděpodobnost přibližně 23 %, pro 20 testů dosahuje pravděpodobnost falešně pozitivního výsledku cca 64 %. Pro problematiku výskytu falešně pozitivních výsledků ve skupině souvisejících testů a jejich kontroly se používá termín Familywise error rate (FWER).

S problémem vícenásobného testování se můžeme setkat ve dvou situacích. První z nich je nesprávně provedené testování ve studiích s více než dvěma skupinami (kategoriemi). Máme-li například v experimentu tři skupiny pokusných zvířat (A - žádný lék, B - starý lék, C - nový lék), můžeme se setkat s chybným testováním rozdílu mezi skupinami pomocí dvouvýběrových testů prováděných po dvojicích, tedy A vs. B, A vs. C, B vs. C. Jsou-li však dílčí testy provedeny na α1=0,05, vzroste celková pravděpodobnost chyby prvního druhu α=1-(1-0,05)3=0,143, tedy přibližně 14 %. Přestože je možné dílčí hodnoty α1 snížit tak, abychom dosáhli požadované hodnoty celkové α (Bonferroniho korekce, Šidákova korekce), není ani po této úpravě testování po dvojicích pro prvotní vyhodnocení dat vhodné a je třeba využít testy, které jsou pro více kategorií navržené (nejčastěji ANOVA – analýza rozptylu).

Druhou situací, kdy má význam se zabývat problémem vícenásobného testování, jsou rozsáhlé explorativní studie, ve kterých jsou často provedeny stovky testů, a je tak téměř nevyhnutelné, že mezi pozitivními výsledky budou některé falešné. Tradiční metody FWER řešící problém vícenásobného testování (například Bonferroniho a Šidákova korekce zmíněné v předchozím odstavci) spočívají ve snížení hladiny významnosti dílčích testů tak, aby bylo dosaženo rozumné celkové hladiny významnosti. V případě rozsáhlých studií (tedy velkého počtu testů) jsou však tyto metody natolik přísné, že neúměrně snižují sílu testů, čímž zvyšují množství falešně negativních výsledků nebo dokonce téměř znemožňují nalezení jakéhokoli pozitivního výsledku vůbec. V poslední době jsou tak často využívány méně striktní metody False discovery rate (FDR), jejichž cílem není eliminace všech falešně pozitivních výsledků, ale pouze jejich udržení v rozumném poměru oproti pravdivým pozitivním výsledkům.

Výběr testu

Z hlediska způsobu výpočtu rozlišujeme testy parametrické, které předpokládají a vyžadují určité rozdělení a/nebo vlastnosti zkoumané veličiny (nejčastěji normální rozdělení, shodné rozptyly) a neparametrické, které podobné předpoklady nevyžadují a vychází pouze z dostupných dat.

Parametrické testy zpravidla nabízí větší sílu, jejich použití je však podmíněno splněním předpokladů a jsou také citlivé vůči odlehlým hodnotám. Vzhledem k předpokladu normálního rozdělení je při jejich využití rozumné volit i příslušné statistiky pro prezentaci výsledků (aritmetický průměr, výběrovou směrodatnou odchylku, střední chybu průměru). Nejsou-li předpoklady parametrických testů splněny nebo obsahují-li data odlehlá pozorování, je vhodné použít vhodnou neparametrickou alternativu (všechny běžné parametrické testy mají své neparametrické protějšky).

Nejběžnější neparametrické metody jsou založené na náhradě změřené hodnoty veličiny pořadím subjektu ve vzorku podle této hodnoty seřazeném. Protože je používáme v případě nenormálně rozdělených veličin nebo přítomnosti odlehlých pozorování, je vhodné ve spojení s nimi volit i odpovídající statistiky (medián, kvartily).

Rozlišení parametrických a neparametrických metod má velký význam při analýze spojitých veličin (jak při jejich porovnávání, tak při zkoumání závislosti např. pomocí korelací), kde budeme při volbě testu vycházet opět vycházet z otázky:

Má zkoumaná veličina normální rozdělení a jsou data prosta odlehlých pozorování?

•ANO – Volíme parametrické metody.

•NE nebo nevíme – Volíme neparametrické metody.

Testy kategorických veličin nakládají s četnostmi a klasifikace na parametrické a neparametrické metody je u nich zpravidla bezpředmětná. Naproti tomu u nich zpravidla rozlišujeme mezi metodami přibližnými, které používají spojité aproximace rozdělení pravděpodobnosti a přesnými, které využívají přímého výpočtu všech kombinací. Přibližné metody usnadňují výpočet u velkých vzorků, kde by byl přesný výpočet obtížný, zatímco přesné metody se uplatňují tam, kde jsou pozorované četnosti malé a přibližné metody neposkytují dostatečnou přesnost.

Nejpodstatnějším kritériem pro volbu statistického testu je však jeho účel, tedy to, jakou vlastnost souboru s jeho pomocí vůbec testujeme. Tato otázka klíčovým způsobem vychází z typu zpracovávaných dat, podle kterého jsou metody roztříděné v následujícím přehledu (kde je to na místě, budeme v něm parametrické a neparametrické metody rozlišovat barevně).

Jedna proměnná (zkoumáme rozdělení veličiny)

•Kvantitativní – Stejně jako existují polohové, disperzní a tvarové statistiky, tak i jednotlivé testy se zaměřují na jednu z těchto vlastností náhodné veličiny.

Poloha

Jednovýběrový studentův t-test (en. one-sample t-test) – Test vynalezený pro sledování kvality v pivovaru Guinness.

Znaménkový test (en. sign test).

Wilcoxon signed rank test – Má větší sílu než znaménkový test, ale vyžaduje symetrické rozdělení veličiny.

Disperze

One-sample chi-square test for variance.

Tvar (normalita) – U testů normality předpokládá nulová hypotéza normální rozdělení, p-hodnota < α tedy značí významně nenormální rozdělení.

Shapiro-Wilk test – Preferovaný test normality s dobrou silou.

Kolmogorov-Smirnov test, Lilliefors test – Alternativní testy normality.

•Kategorická – Kategorické proměnné vykazují pouze četnosti jednotlivých kategorií, a proto u nich není možné definovat polohu ani disperzi. U jedné kategorické proměnné tak můžeme testovat pouze skutečnost, zda má určité rozdělení či nikoli, a to prostřednictvím srovnání pozorovaných a očekávaných četností.

Pearsonův chí-kvadrát test – Přibližný test využívající výpočtu statistiky, jejíž rozdělení se blíží spojitému rozdělení chí-kvadrát.

Přesné testy – Podobně jako v příkladu s kostkou uvedeném v oddílu 5.1 můžeme v jednoduchých případech vyjít přímo z definice p-hodnoty a určit ji sečtením přesných okrajových pravděpodobností vypočtených na základě předpokládaného rozdělení veličiny (nulové hypotézy).

Dvě proměnné (zkoumáme závislost nebo rozdíl veličin)

•Dvojice kvantitativních veličin

Závislost – Zpravidla zkoumáme, zda mezi hodnotami obou veličin existuje závislost či nikoli. Nejčastější metodou je výpočet korelace mezi hodnotami veličin. V případě korelačních matic sice výsledek zahrnuje více proměnných, ale jednotlivé výpočty jsou prováděné vždy po dvojicích a stále se jedná o zjištění závislosti mezi dvěma veličinami.

Je nutné poznamenat, že statisticky významná korelace mezi veličinami ještě neznamená jejich kauzální spojení, protože obě veličiny mohou být podmíněné společnými faktory, aniž by spolu přímo souvisely. Pokud bychom například zjistili, že průměrné množství ročně zkonzumovaného piva významně koreluje s délkou vlasů, nemůžeme výsledek interpretovat tak, že pití piva růst vlasů ovlivňuje. Krom skutečnosti, že příčinný vztah může být i opačný, a sice že délka vlasů nějakým způsobem ovlivňuje náklonnost k pivu, také přímý kauzální vztah mezi veličinami nemusí existovat vůbec. V tomto případě by se nejspíše jednalo o nepodchycenou souvislost obou veličin s pohlavím, neboť ženy mají zpravidla delší vlasy a pijí méně piva.

Analýza korelace veličin má dvě složky. Samotný výpočet korelačního koeficientu udává těsnost odhalené souvislosti, ale nevypovídá o její statistické významnosti. Následný test významnosti poskytuje p-hodnotu, podle které naopak není možné určit sílu závislosti mezi veličinami. Stejně jako při rozlišení klinické a statistické významnosti ostatních výsledků je třeba i u korelací odhalit zejména situace, kdy mezi veličinami vypozorujeme silnou korelaci, která není významná (většinou kvůli malému vzorku), anebo v praxi častější případ, kdy je souvislost veličin statisticky významná, ale slabá.

Pearsonův korelační koeficient – Udává, jak silnou lineární (!) závislost je mezi veličinami možné nalézt. Jeho hodnota vypočtená ze vzorku (tedy odhad populační hodnoty ρ) se zpravidla označuje r. Nabývá hodnot od -1 (zcela ideální lineární závislost ve smyslu čím více – tím méně) přes 0 (žádná závislost) až po 1 (zcela ideální lineární závislost ve smyslu čím více – tím více). Jako parametrická metoda je obzvláště citlivý vůči odlehlým pozorováním, která je při jeho použití nezbytné důsledně eliminovat. Při jeho výpočtu nezáleží na pořadí veličin, r vypočtené mezi veličinami X a Y je shodné s r pro veličiny Y a X.

Spearmanův korelační koeficient – Využívá náhrady naměřených hodnot pořadím subjektu. Je schopen odhalit jakoukoli monotónní závislost mezi veličinami bez ohledu na její tvar. Nabývá stejných hodnot jako Pearsonův korelační koeficient s obdobným významem (-1 pro dokonalou rostoucí monotónní závislost, 0 pro žádnou souvislost a 1 pro dokonalou rostoucí monotónní závislost).

Kendallovo tau, Goodmanova a Kruskalova gamma – Další korelační statistiky založené na pořadí.

Závislá (párová) pozorování – Tvoří-li dvojice veličin závislá pozorování, můžeme také testovat, zda se tyto veličiny významně liší (tedy například došlo-li k významnému nárůstu tkáně po aplikaci růstových faktorů). K tomuto účelu využíváme párové testy polohy. Testy, které zde uvedeme, se shodují s polohovými testy pro jednu kvantitativní proměnnou, neboť zpracování párových pozorování spočívá ve výpočtu jejich rozdílu, jehož poloha je následně otestována vůči nulové (zero) nulové (null) hypotéze.

Studentův t-test pro závislá pozorování

Znaménkový test (en. sign test).

Wilcoxon signed rank test – Jeho aplikace na závislá pozorování bývá někdy označována také jako Wilcoxon matched pairs test.

•Dvojice kategorických veličin – I v tomto případě zkoumáme souvislost mezi veličinami, tedy zdali příslušnost subjektu do určité kategorie jedné veličiny ovlivňuje pravděpodobnost, že bude v určité kategorii veličiny druhé (například zda je mezi muži více kuřáků než mezi ženami). Vzhledem k tomu, že vstupem testů jsou četnosti kombinací jednotlivých kategorií (tedy kontingenční tabulka) bývají tyto testy označované jako testy kontingenčních tabulek. S těmi sdílí i tu vlastnost, že výsledek testu nezáleží na uspořádání veličin, tedy pro test souvislosti mezi pohlavím a kouřením (kuřák/nekuřák) existuje jediný test bez ohledu na to, zda položíme otázku „Jsou muži častěji kuřáky?“, nebo „Jsou kuřáci častěji muži?“.

Chí-kvadrát test – Přibližný test využívající spojité aproximace rozdělení statistiky testu. K odhadu očekáváných četností využívá řádkové a sloupcové součty v kontingenční tabulce. Je použitelný pro kontingenční tabulku libovolné velikosti, četnosti ve všech jejích buňkách však musí být vyšší než 10. Především pro malé vzorky se můžeme setkat jeho doplněním Yatesovou korekcí, jejíž využití je však v poslední době (především díky rostoucím výpočetním kapacitám pro přesné testy) omezené.

Fisherův přesný test – Jak napovídá jeho název, jedná se o přesný test, tedy vypočítává a sčítá pravděpodobnosti všech okrajových kombinací četností. Měli bychom jej využít, obsahuje-li kontingenční tabulka buňku s četností 10 a méně, nicméně tato hranice je čistě empirická. Ve své původní podobě je definován jen pro kontingenční tabulky velikosti 2x2.

Další přesné testy – Výpočetní výkon v dnešní době umožňuje provedení přesných testů (jedná se zpravidla o rozšíření Fisherova testu) pro čím dál větší kontingenční tabulky a početnější vzorky, čímž je možné se vyhnout poměrně zásadnímu omezení Fisherova testu na velikost kontingenční tabulky 2x2. Přestože je to teoreticky možné, není vhodné tyto testy využívat na velmi rozsáhlé kontingenční tabulky (mnoho kategorií) s nízkými četnostmi (malý vzorek), tato situace zpravidla vyžaduje změnu schématu experimentu (např. sloučení podobných kategorií). Nemalou překážkou v použití těchto testů je také fakt, že v řadě programů pro zpracování dat nejsou nativně obsažené.

•Kategorická a spojitá – Tato kombinace proměnných představuje nejčastější situaci, se kterou se při testování hypotéz setkáváme. Subjekty v našem vzorku jsou v tomto případě rozděleny do skupin, mezi nimiž hledáme rozdíly v kvantitativní veličině. Kategorickou proměnnou pak představuje právě příslušnost vzorku ke skupině. Při porovnání se opět můžeme věnovat různým vlastnostem rozdělení kvantitativní veličiny, typicky poloze nebo disperzi. Důležitým faktorem je také počet kategorií, které srovnáváme.

Dvě kategorie – Dvouvýběrové testy (two-sample tests)

Poloha

•Studentův t-test (two sample t-test) – Zřejmě neznámější statistický test vůbec. V základní variantě předpokládá, že spojitá veličina má v obou kategoriích stejný rozptyl, což zpravidla nejprve ověřujeme pomocí F-testu. Pro případ nestejných rozptylů využíváme alternativní variantu, která je bez problémů dostupná ve většině softwarových produktů.

•Mann-Whitney U test – Nazýván také Mann-Whitney-Wilcoxon test a Wilcoxon rank-sum test. Jedná se o nejpoužívanější neparametrický test polohy.

Poloha a tvar zároveň – Předpokládá-li nulová hypotéza, že vzorky obou kategorií pocházejí ze stejného rozdělení (namísto předpokladu dvou rozdělení se stejnou polohou), může k jejímu zamítnutí dojít jak z důvodu odlišné polohy, tvaru rozdělení i kombinace obého. To je případ i následujících neparametrických testů.

•Wald-Wolfowitz runs test.

•Kolmogorov-Smirnov test.

Disperze

•F-test – Testuje významnost rozdílu mezi rozptyly dvou kategorií s normálním rozdělením spojité veličiny. Často je využíván před provedením t-testu pro volbu jeho správné varianty.

Více kategorií – V oddílu 5.4 jsme již vysvětlili, proč není možné pro porovnání více kategorií použít dvouvýběrové testy a proč je tedy v situacích s více proměnnými nutné využít testy k tomu učené. Tyto testy vychází z nulové hypotézy formulované pro všechny kategorie zároveň (například střední hodnota v kategorii A, B a C se neliší) a její zamítnutí proto neposkytuje informaci, mezi kterými skupinami se rozdíl nachází (můžeme pouze tvrdit, že hodnoty v kategoriích A, B a C nepochází z rozdělení se stejnou střední hodnotou).

Poloha

•Jednofaktorová analýza rozptylu (ANOVA) (en. one-way ANalysis Of VAriance) – Přestože se v názvu hovoří o rozptylu, jedná se o test polohy. Rozptyl je totiž použit při výpočtu, kdy jsou srovnávány rozptyly uvnitř kategorií s rozptylem celého vzorku napříč kategoriemi. Důležitými předpoklady ANOVY jsou normální rozdělení zkoumané veličiny a homogenita (tedy rovnost) rozptylů v rámci kategorií. Pro určení, mezi kterými kategoriemi se rozdíl vyskytuje rozdíl, používáme tzv. post-hoc testy (např. Schefféův, Fisherův, Bonferonniho).

•Kruskal-Wallis ANOVA – Je rozšířením Mann-Whitney U testu pro více kategorií, čímž představuje neparametrickou obdobu jednofaktorové ANOVY.

•Mediánový test – Alternativa ke Kruskal-Wallis ANOVĚ, zpravidla však s menší silou. Využívá Pearsonova chí-kvadrát testu v kontingenční tabulce četností pozorování v jednotlivých kategoriích, která jsou větší a menší než celkový medián veličiny ve vzorku.

Disperze (rozptyl) – Testy pro porovnání rozptylů ve více skupinách jsou zpravidla používány pro ověření podmínky homogenních rozptylů před provedením ANOVY.

•Levene’s test

•Brown-Forsythe test

•Barlett’s test

Více proměnných

•Závislost spojité proměnné na více kategorických proměnných

Vícefaktorová ANOVA – Rozeznáváme variantu s interakcemi (každá kombinace kategorií může mít specifický efekt) a bez interakcí (kategorické veličiny se neovlivňují).

•Závislost spojité proměnné na více spojitých proměnných nebo kombinaci spojitých a kategorických proměnných

Obecné lineární modely, zobecněné lineárními a nelineární modely – Můžeme je vnímat jako rozšíření ANOVY pro ověřování komplexních hypotéz.

ANCOVA – Analýza kovariance (en. ANalysis of COVAriance). Typ obecného lineárního modelu kombinující přístupy ANOVy a regresních modelů.

Regresní modely – Přestože k tomu nejsou primárně určené, jsou regresní modely (např. vícenásobná lineární regrese) schopné poskytnout p-hodnoty pro jednotlivé vstupní proměnné.

•Závislost více spojitých proměnných na jedné či více nezávisle proměnných

MANOVA – Multivariační ANOVA (en. Multivariate ANalysis Of VAariance. Multivariační statistika se zabývá sledováním a analýzou více výsledných (závisle) proměnných současně. MANOVA je testovací metoda porovnávající multivariační střední hodnoty v několika skupinách.

•Více závislých pozorování, kombinace závislých pozorování s dalšími vlivy – Opět jde zpravidla o komplexní experimentální uspořádání.

ANOVA pro opakovaná pozorování (en. repeated measures ANOVA) – Můžeme ji využít, máme-li v experimentu více než dvě závislá pozorování, případně i v kombinaci s dalšími faktory.

Friedmanova ANOVA – Používáme pro více než dvě závislá pozorování.

•Vícerozměrné metody – přestože se již nejedná o nástroje pro testování hypotéz, můžeme zmínit, že oblasti více proměnných se věnuje i celá řada přístupů a metod pro průzkum vícerozměrných dat a problémů, jako jsou například shlukování, klasifikační a regresní stromy, analýza hlavních komponent, faktorová analýza apod.

Analýza přežití

Povaha zpracovávaných dat

Při zpracování dat z klinických studií je jedním z nejčastěji vyhodnocovaných indikátorů doba přežití jednotlivých subjektů – pacientů. Nemusí se přitom jednat přímo o přežití jako takové, stejný charakter mají i další klinické ukazatele, které vystihují čas uplynutý do nějaké události, například čas od léčebného zákroku do relapsu onemocnění. Mezi nejčastěji vyhodnocované charakteristiky patří:

•Overall survival (OS) – Doba od diagnózy, zahájení léčby nebo operace, po kterou subjekt žil.

•Disease-specific survival (DSS) – Čas do úmrtí způsobeného zkoumaným onemocněním.

•Disease-free survival (DFS), disease-free interval (DFI) – Doba od léčebného zákroku, po kterou je onemocnění v remisi.

•Progression-free survival (PFS) – Doba, po kterou je onemocnění stabilní, bez progrese.

V praxi je možné definovat řadu dalších obdobných intervalů. Jejich přesné vymezení je nezbytné pro správné zpracování dat a výpočet samotných intervalů, na následnou analýzu nicméně klinický význam daného intervalu vliv nemá, všechny obdobné ukazatele zpracováváme stejným způsobem. Obecným znakem všech ukazatelů zpracovávaných pomocí analýzy přežití (ať už v medicíně nebo technických oborech) je, že udávají délku intervalu do události, která může pro daný subjekt nastat pouze jednou, neboť trvale změní jeho stav (úmrtí pacienta, relaps onemocnění, selhání elektronické součástky, prasknutí žárovky apod.).

Proč potřebujeme analýzu přežití?

V této části představíme dva hlavní důvody, proč je nezbytný speciální analytický aparát pro zpracování dat přežití.

Cenzorovaná pozorovaní

Prvním důvodem vzniku metod pro analýzu přežití je skutečnost, že v době ukončení studie zpravidla neznáme dobu přežití pro všechny subjekty – někteří pacienti v době ukončení ještě žijí, s jinými ztratíme kontakt (například se odstěhují), další mohou zemřít z příčin nesouvisejících s onemocněním (například při autonehodě). Pro tyto pacienty však zpravidla známe jistou dobu, po kterou prokazatelně žili. Takové pozorování nazýváme cenzorované. I cenzorovaná pozorování mají jistou informační hodnotu, kterou bychom s běžnými statistickými metodami nedokázali využít, zatímco analýza přežití je pro jejich výskyt navržena. Vznik cenzorovaných pozorování v rámci studie je znázorněn na Obr. 17.

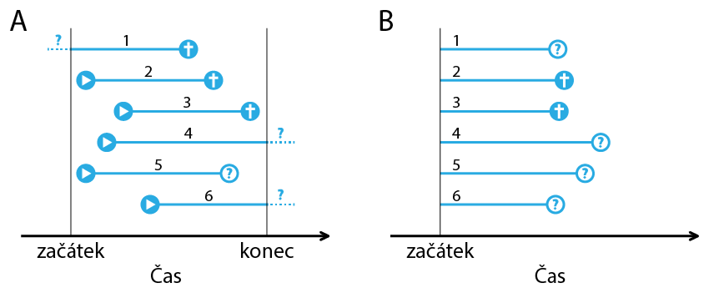
$Cenzorování v průběhu studie. A – skutečný průběh studie, do které jsou průběžně rekrutováni pacienti (případně jde o retrospektivní studii v daném čase). B – pohled na stejné pacienty z hlediska analýzy přežití. Pro pacienta č. 1 nastala počáteční událost (např. operace) v neznámém bodě před začátkem studie. Protože ale víme, že během studie prokazatelně žil po jistou dobu až do zaznamenaného úmrtí, pohlížíme na něho jako na cenzora. U pacientů 2 a 3 známe přesně počáteční i terminální bod, jedná se ukončená pozorování. Pacienti 4 a 6 v době ukončení studie ještě žili, představují proto cenzorovaná pozorování. S pacientem č. 5 byl v průběhu studie ztracen kontakt – opět se jedná o cenzorované pozorování. C:\Users\hosek\Disk Google\_BC\OPVK\PART 1+2\Obrázky CZ\censoring.png$

Obrázek 17: Cenzorování v průběhu studie. A – skutečný průběh studie, do které jsou průběžně rekrutováni pacienti (případně jde o retrospektivní studii v daném čase). B – pohled na stejné pacienty z hlediska analýzy přežití. Pro pacienta č. 1 nastala počáteční událost (např. operace) v neznámém bodě před začátkem studie. Protože ale víme, že během studie prokazatelně žil po jistou dobu až do zaznamenaného úmrtí, pohlížíme na něho jako na cenzora. U pacientů 2 a 3 známe přesně počáteční i terminální bod, jedná se ukončená pozorování. Pacienti 4 a 6 v době ukončení studie ještě žili, představují proto cenzorovaná pozorování. S pacientem č. 5 byl v průběhu studie ztracen kontakt – opět se jedná o cenzorované pozorování.

V praxi se nejčastěji setkáme s pozorováními cenzorovanými zprava, kdy víme, že skutečná hodnota je vetší než délka cenzorovaného pozorování, ale nevíme o kolik. V případě cenzorování zleva je situace opačná – cenzorované pozorování představuje maximální možnou skutečnou délku přežití.

Použití cenzorovaných pozorování však není zcela bezproblémové. Pro dosažení validních výsledků by jich nemělo být ve vzorku příliš (jako akceptovatelná hranice se uvádí cca 30 %), což je možné ověřit snadným výpočtem. Druhým předpokladem je, že délka cenzorovaného pozorování by měla být nezávislá na skutečném přežití subjektu (neboli subjekty s krátkým i dlouhým přežitím by měly mít stejnou šanci stát se cenzory), což se ověřuje a zajišťuje obtížněji (Leung, Elashoff a Afifi, 1997).

Žijeme jen jednou

Samozřejmá skutečnost, že u každého pacienta můžeme úmrtí pozorovat nejvýše jednou, má za následek, že vzorek, ve kterém můžeme výskyt události pozorovat, se v čase zmenšuje. Díky tomu mají pozorované časy přežití jako náhodná veličina specifický charakter. Představíme-li si vzorek pacientů, kteří mají v čase konstantní riziko úmrtí, budeme nejvíce zemřelých zaznamenávat na samém počátku studie. S tím, jak bude subjektů ubývat, bude klesat i množství zaznamenaných událostí, přestože riziko je stále stejné. V drtivé většině případů proto rozdělení časů přežití nevykazuje žádnou typickou hodnotu, kterou bychom mohli považovat za vhodnou polohovou statistiku (interpretace průměrného přežití nebo mediánu přežití proto může být zavádějící). Z tohoto důvodu je definováno několik odvozených ukazatelů popisujících přežití subjektů ve vzorku, které nám umožní výsledky snáze interpretovat. Jedním z nich je míra rizika (hazard rate, rovněž riziko nebo riziková funkce), která má charakter podmíněné pravděpodobnosti (pravděpodobnost výskytu události v daném čase za předpokladu, že se dosud nestala). Přehled funkcí popisujících přežití je uveden na Obr. 18.

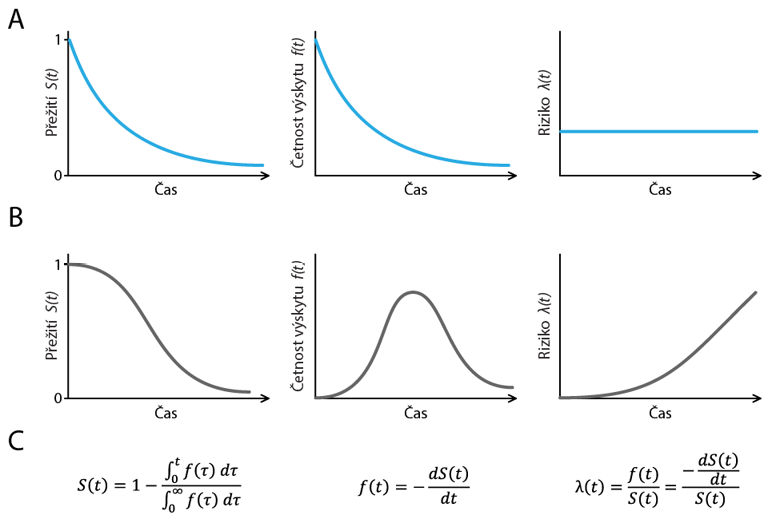
$Funkce popisující přežití. Průběh funkcí relativního přežití (S), četnosti zaznamenaných událostí (f, odpovídá rozdělení času přežití ve vzorku, což jsou zpravidla naše výchozí data) a míry rizika (λ) v čase. A – konstantní riziko. Vidíme, že četnost pozorování události v čase klesá, neexistuje typická hodnota. Podobný scénář je v praxi častější. B – situace, v níž existuje typická doba přežití (vyobrazení se blíží normálnímu rozdělení). V tomto případě bychom pozorovali esovitý průběh křivky přežití. Za povšimnutí stojí, že riziko může růst i pokud počet zaznamenaných událostí klesá. C – vzorce popisující vzájemný vztah uvedených proměnných. C:\Users\hosek\Disk Google\_BC\OPVK\PART 1+2\Obrázky CZ\deskriptory.png$

Obrázek 18: Funkce popisující přežití. Průběh funkcí relativního přežití (S), četnosti zaznamenaných událostí (f, odpovídá rozdělení času přežití ve vzorku, což jsou zpravidla naše výchozí data) a míry rizika (λ) v čase. A – konstantní riziko. Vidíme, že četnost pozorování události v čase klesá, neexistuje typická hodnota. Podobný scénář je v praxi častější. B – situace, v níž existuje typická doba přežití (vyobrazení se blíží normálnímu rozdělení). V tomto případě bychom pozorovali esovitý průběh křivky přežití. Za povšimnutí stojí, že riziko může růst i pokud počet zaznamenaných událostí klesá. C – vzorce popisující vzájemný vztah uvedených proměnných.

Nejběžnější metody analýzy přežití

Metoda Kaplan-Meier

Metoda Kaplan-Meier je nejčastěji používaným způsobem odhadu funkce přežití (S) z časů přežití jednotlivých subjektů (f), mezi nimiž jsou přítomna cenzorovaná pozorování. Způsob výpočtu je poměrně jednoduchý. Mějme vzorek čítající n pacientů. Funkce přežití začíná v čase 0 na hodnotě 1, na níž zůstává až do času odpovídajícímu prvnímu pozorování. Je-li toto pozorování ukončené (není cenzorované), klesne v tomto čase hodnota funkce přežití o 1/n, což je podíl vzorku odpovídající jednomu pacientovi. Hodnota funkce přežití by tedy klesla na 1-1/n = (n-1)/n. Narazíme-li kdykoli v průběhu výpočtu na pozorování cenzorované, rozpočítá se aktuální zbývající hodnota funkce přežití mezi ostatní žijící pacienty, čímž se zvýší podíl jednoho pacienta pro další výpočet. Hodnota funkce přežití se přitom nezmění. Pokud bychom tedy na cenzorované pozorování narazili hned jako první, upravili bychom váhu jednoho pacienta na z 1/n na 1/(n-1) a pokračovali dále s hodnotou funkce přežití 1. Pokud by bylo cenzorované až druhé pozorování, vyšli bychom z výše vypočtené hodnoty přežití po prvním zemřelém pacientovi (n-1)/n, na níž by funkce přežití setrvala, ale váhu jednoho pacienta bychom upravili na ((n-1)/n)/(n-2).

Výhodou této metody je, že nepředpokládá žádné vlastnosti ani tvar funkce přežití, vychází pouze z dostupných dat. Můžeme ji tedy považovat za metodu neparametrickou. Nevýhodou s tím spojenou je fakt, že výsledný odhad funkce přežití není hladký, ale má schodovitý průběh, který není bez dalších úprav možné analyticky zpracovat jako matematickou funkci.

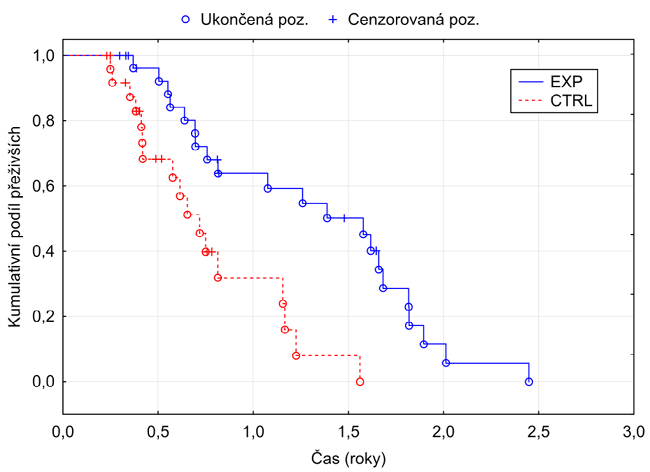
$Kaplanův-Meierův odhad funkce přežití – srovnání dvou skupin. C:\Users\hosek\Disk Google\_BC\OPVK\PART 1+2\Obrázky CZ\Kaplan-Meier\Graph in kaplan-meier.stw.png$

Obrázek 19: Kaplanův-Meierův odhad funkce přežití – srovnání dvou skupin

Odhady funkcí přežití získané pomocí Kaplanovy-Meierovy metody umožňují při vykreslení do jednoho grafu snadné vizuální porovnání přežití v různých skupinách (viz Obr. 19). Zkušený pozorovatel získá z výšky skoků v průběhu funkce také představu o velikosti vzorku. Významnost rozdílu mezi skupinami je možné zkoumat pomocí řady statistických testů, např. Gehan-Wilcoxon, Cox-Mantel nebo Log rank. Síla těchto testů se liší v závislosti na velikosti vzorku a rozdělení přežití pacientů. Gehan-Wilcoxon test také klade větší důraz na počátky křivek, zatímco v Log rank testu je větší váha přisuzována pozdějším fázím studie.

Regresní modely

Budeme-li předpokládat, že rozdělení časů přežití v našem vzorku odpovídá některému definovanému rozdělení pravděpodobnosti (nejčastěji exponenciálnímu nebo Weibullovo), můžeme na základě tohoto rozdělení vytvořit model funkce přežití. Chceme-li posoudit, koreluje-li jedna nebo více nezávisle proměnných s přežitím pacientů, vytvoříme na základě známého předpokládaného rozdělení regresní model predikující tvar hypotetické funkce přežití pacientů s danou hodnotou nebo kombinací hodnot nezávisle proměnných (regresorů). Porovnáním optimalizovaného regresního modelu s modelem nulovým (nejlepší model, který zkoumané nezávislé proměnné nebere v potaz) pak můžeme získat p-hodnotu odpovídající nulové hypotéze, že zvolené regresory s přežitím pacientů nekorelují. Vzhledem k tomu, že předpokládáme určité rozdělení zkoumané veličiny, řadíme tyto modely mezi metody parametrické.

Protože je nutnost předpokládat určitý tvar rozdělení časů přežití v praxi poněkud limitující, bývá namísto parametrických modelů přežití častěji využíván Coxův model proporcionálních rizik, který žádný předpoklad o rozdělení přežití pacientů nevyžaduje. Operuje pouze s úvahou, že existuje určitá neznámá výchozí riziková funkce, jejíž hodnota se škáluje úměrně k hodnotám regresorů. Z pohledu rozdělení přežití se tak jedná o metodu neparametrickou, avšak z pohledu regrese samotné (tedy změny rizika v závislosti na hodnotách nezávisle proměnných) je předpokládána definovaná (log-lineární) závislost, což odpovídá parametrickému přístupu. Z tohoto důvodu se můžeme setkat z označením Coxova modelu proporcionálních rizik za metodu semiparametrickou.

Nejvýznamnějším předpokladem Coxova modelu proporcionálních rizik je však samotná proporcionalita rizika neboli časová nezávislost poměru rizika u skupin s danými hodnotami regresorů. Při změně hodnoty nezávisle proměnné se tedy riziková funkce škáluje konstantním koeficientem ve všech časových bodech. Tento předpoklad je poměrně zásadní a v řadě studií nemusí být splněn. Porovnáváme-li například chirurgickou a medikamentózní léčbu, je pravděpodobné, že v důsledku komplikací bude riziko krátce po operaci vyšší než v případě léčby medikamentózní, zatímco z dlouhodobějšího hlediska tomu tak být již nemusí. Pro tyto případy existuje i alternativní Coxův model zahrnující časovou závislost efektu regresorů.

Velkou předností všech zmíněných regresních modelů je skutečnost, že jako nezávisle proměnné můžeme použít i proměnné spojité, což testy významnosti pro porovnání skupin popsané v sekci 6.3.1 neumožňují (můžeme pro jejich použití sice subjekty roztřídit do několika skupin podle hodnoty proměnné, ale to rozhodně není ideální).

Vhodným způsobem prezentace výsledků za účelem jejich snadné interpretace je využití popsaných regresních modelů pro odhad poměru rizik (hazard ratio) mezi skupinami nebo v závislosti na určité změně nezávisle proměnné. Jedná se jednoduše o poměr hodnot rizikových funkcí (hazard rates). Použijeme-li k odhadu regresní model předpokládající konstantní poměr rizik v čase (např. Coxův model proporcionálních rizik), obdržíme logicky jedinou hodnotu, jejíž platnost pro celé zkoumané časové období závisí právě na platnosti předpokladu proporcionálních rizik. Použijeme-li naopak model s časově proměnnými kovariáty, bude poměr rizik funkcí času. Zmíněné modely umožňují vypočítat poměr rizik včetně intervalu spolehlivosti, který nám umožní snadno rozeznat statisticky významné snížení či zvýšení rizika.

Citovaná literatura:

HOENIG, J. M. a HEISEY, D. M. (2001) The Abuse of Power: The Pervasive Fallacy of Power Calculations for Data Analysis. The American Statistician. 55(1). p. 1–6.

LEUNG, K. M., ELASHOFF, R. M. a AFIFI, A. A. (1997) Censoring issues in survival analysis. Annu Rev Public Health. 18. p. 83–104.

1 Pozor, případem takového neznámého činitele je i nepostihnutá variabilita jednotlivých subjektů ve statistickém vzorku, což nám může z počátku připadat zvláštní. Měříme-li totiž tělesný vzrůst náhodně vybraných osob, je nám dopředu jasné, že se hodnoty budou lišit, protože každý člověk je jinak vysoký.

Statistika

Obsah

Co je to statistika?

Význam slova statistika

Co statistika řeší?

Pravděpodobnost a statistika

Data a jejich typy

Co jsou to data?

Kategorie dat

Zaznamenávání a ukládání dat

Problematické jevy v datech

Statistická rozdělení

Rozdělení pravděpodobnosti, statistiky a parametry

Centrální limitní věta a normální rozdělení

Vlastnosti normálního rozdělení

Statistiky a parametry normálního rozdělení

Výběr statistik pro vyhodnocení a prezentaci dat

Prezentace a vizualizace dat

Vizualizace četnosti

Sloupcové grafy

Symbolové grafy

Krabicové grafy

Histogram

Hroznový graf

Bodové grafy (scatter plots)

Grafy více než dvou kvantitativních veličin

Zobrazení posloupností

Testování hypotéz

Principy testování

Chyby, síla a spolehlivost testů

Volba jednostranného či oboustranného testu (en. one-tailed vs. two-tailed)

Problém vícenásobného testování

Výběr testu

Analýza přežití

Povaha zpracovávaných dat

Proč potřebujeme analýzu přežití?

Cenzorovaná pozorovaní

Žijeme jen jednou

Nejběžnější metody analýzy přežití

Metoda Kaplan-Meier

Regresní modely

Citovaná literatura: